标签:
7号晚听了邹博一次微课,正好是自己最近正在死磕的动态规划,所以搬好小板凳听邹博讲解动态规划。现将内容整理如下:
内容主要分为两个部分:
1. 动态规划和贪心的认识——工具:马尔科夫过程
2. 动态规划,通过3个DP中的经典问题详细讲解
1)最长递增子序列LIS
2)格子取数/走棋盘问题及应用
3)找零钱/背包问题
正题开始。首先,人们认识事物的方法有三种:通过概念(即对事物的基本认识)、通过判断(即对事物的加深认识)、和推理(对事物的深层认识)。其中,推理又包含归纳法和演绎法。(这些从初中高中一直到大学我们都是一直在学习的,关键是理解)
归纳法是从特殊到一般,属于发散思维;(如:苏格拉底会死;张三会死;李四会死;王五会死……,他们都是人。所以,人都会死。)
演绎法是从一般到特殊,属于汇聚思维。(如:人都会死的;苏格拉底是人。所以,苏格拉底会死。)
那么,如何用归纳法解决数学问题,进行应用呢?
已知问题规模为n的前提A,求解一个未知解B。(我们用An表示“问题规模为n的已知条件”)
此时,如果把问题规模降到0,即已知A0,可以得到A0->B.
然而,Ai与Ai+1往往不是互为充要条件,随着i的增加,有价值的前提信息越来越少,我们无法仅仅通过上一个状态得到下一个状态,因此可以采用如下方案:
上述两种状态转移图如下图所示:
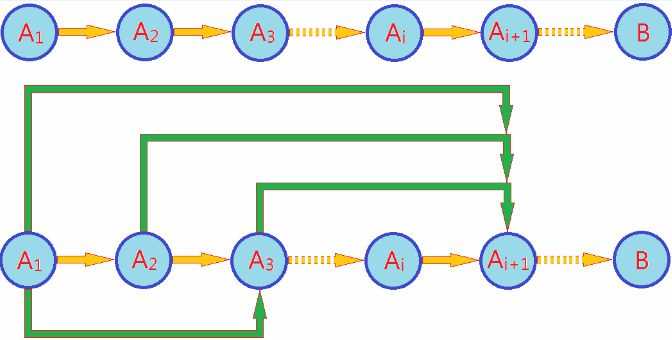
下面通过分析几个经典问题来理解动态规划。
实例一:最长递增子序列(Longest Increasing Subsequence)。
问题描述。给定长度为N的数组A,计算A的最长单调递增的子序列(不一定连续)。如给定数组A{5,6,7,1,2,8},则A的LIS为{5,6,7,8},长度为4.
思路:因为子序列要求是递增的,所以重点是子序列的起始字符和结尾字符,因此我们可以利用结尾字符。想到:以A[0]结尾的最长递增子序列有多长?以A[1]结尾的最长递增子序列有多长?……以A[n-1]结尾的最长递增子序列有多长?分析如下图所示:
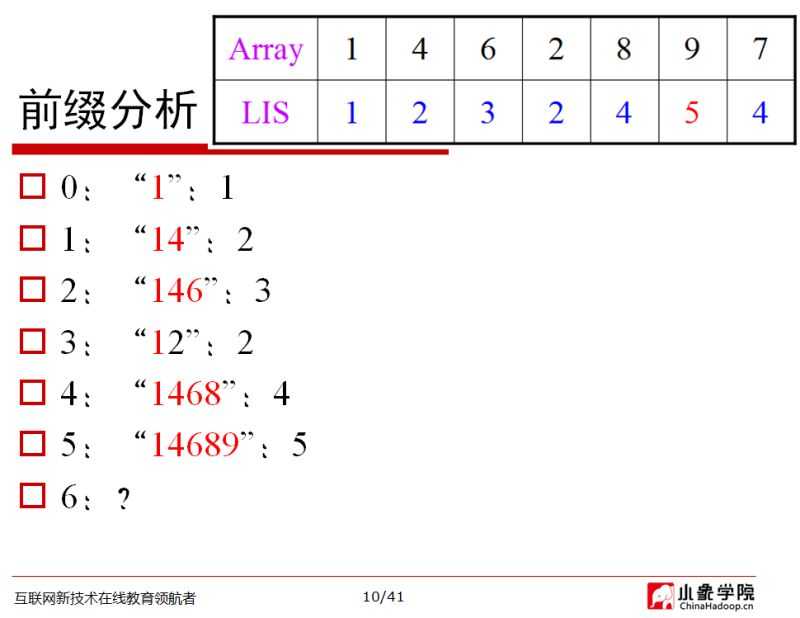
显然,如果ai>=aj,则可以将ai放到b[j]的后面,得到比b[j]更长的子序列。从而:b[i] = max{b[j]}+1. s.t. A[i] > A[j] && 0 <= j < i.
所以计算b[i]的过程是,遍历b[i]之前的所有位置j,找出满足关系式的最大的b[j].
得到b[0...n-1]之后,遍历所有的b[i]找到最大值,即为最大递增子序列。 总的时间复杂度为O(N2).
我实现的Java版代码为:

publi int LIS(int[] A) { if(A == null || A.length == 0) return 0; int[] b = new int[A.length]; b[0] = 1; int result = 1; for(int i=1; i<A.length; i++) { int max = -1; for(int j=0; j<i; j++) { if(A[j] < A[i] && b[j] > max) max = b[j]; } b[i] = max + 1; result = Math.max(result, b[i]); } return result; }
进而,如果不仅是求LIS的长度,而要求LIS本身呢?我们可以通过记录前驱的方式,从该位置找到其前驱,进而找到前驱的前驱……
Java代码如下:

public static ArrayList<Integer> LISDetail(int[] A) { if(A == null || A.length == 0) return null; int[] b = new int[A.length]; int[] b1 = new int[A.length]; b[0] = 1; b1[0] = -1; int result = 1; int index = 0; for(int i=1; i<A.length; i++) { int max = 0; boolean flag = false; for(int j=0; j<i; j++) { if(A[j] < A[i] && b[j] > max) { flag = true; max = b[j]; b1[i] = j; } } if(flag == false) b1[i] = -1; b[i] = max + 1; if(result < b[i]) { result = b[i]; index = i; } } ArrayList<Integer> res = new ArrayList<Integer>(); //res.add(A[index]); for(;index >=0; ) { res.add(A[index]); index = b1[index]; } Collections.reverse(res); return res; }
使用动态规划方法的到O(N2)的时间复杂度算法,能否有更优的方法呢?
最开始,缓冲区里为空;
看到了字符“1”,添加到缓冲区的最后,即缓冲区中是“1”;
看到了字符“4”,“4”比缓冲区的所有字符都大,因此将“4”添加到缓冲区的最后,得到“14”;
看到了字符“6”,“6”比缓冲区的所有字符都大,因此将“6”添加到缓冲区的最后,得到“146”;
看到了字符“2”,“2”比“1”大,比“4”小,因此将“4”直接替换成“2”,得到“126”;
看到了字符“8”,“8”比缓冲区的所有字符都大,因此将“8”添加到缓冲区的最后,得到“1268”;
看到了字符“9”,“9”比缓冲区的所有字符都大,因此将“9”添加到缓冲区的最后,得到“12689”;
看到了字符“7”,“7”比“6”大,比“8”小,因此将“8”直接替换成“7”,得到“12679”;
现在,缓冲区的字符数目为5,因此,数组A的LIS的长度就是5!
这样,时间复杂度变为每次都在一个递增的序列中替换或插入一个新的元素,所以为O(nlogn)。
代码为:

public int len = 0; public int LIS1(int[] A) { if(A == null || A.length == 0) return 0; int[] b = new int[A.length]; b[0] = A[0]; len = 1; for(int i=1; i<A.length; i++) { insert(b, A[i]); } return len; } public int[] insert(int[] a, int val) { if(val < a[0]) { a[0] = val; return a; } if(val > a[len-1]) { a[len] = val; len++; return a; } int left = 0, right = len-1, mid = (left + right) / 2; while(left < right) { mid = (left + right) / 2; if(a[mid] < val && a[mid+1] >= val) { a[mid+1] = val; return a; } if(a[mid] >= val && a[mid-1] < val) { a[mid] = val; return a; } if(a[mid] < val) left = mid+1; if(a[mid] > val) right = mid-1; } return a; }
但后来我分析了这种方法只能得到长度,不能得到子序列本身。(老师上课时提示说考虑序列长度变化的时候,对于示例数组{1,4,6,2,8,9,7}来说可以解决,即当序列变长的时候,元素1,4,6,8,9正好是最终的字长递增子序列;当如果原数组是{10,9,2,5,3,7,101,18}时,就不是这么回事了。目前我没有找到求解子序列本身的方法,留作以后思考。)
实例二:格子取数/走棋盘问题
问题描述。给定一个m*n的矩阵,每个位置是一个非负整数,从左上角开始放一个机器人,它每次只能朝右和下走,走到右下角,求机器人的所有路径中,总和最小的那条路径。如下图所示,其中图中所示的彩色方块是已知的某些非负整数值。

考虑一般情况下位于机器人位于某点(x, y)处,那么它是怎么来的呢?只可能来自于左边或者上边。即:
dp[x, y] = min(dp[x-1, y], dp[x, y-1]) + a[x, y],其中a[x, y]是棋盘中(x, y)点的权重取值。
然后考虑位于最左边一列与左上边的一行,得到所有的状态转移方程为:
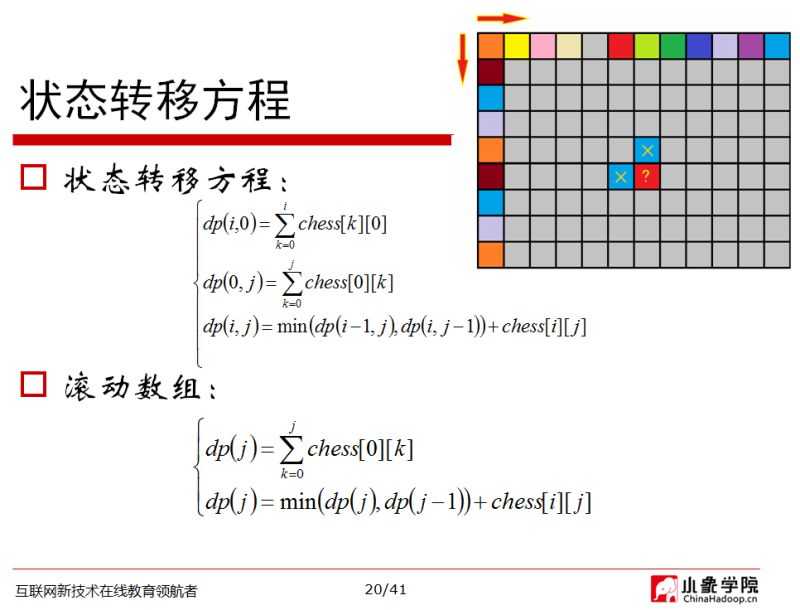
所以,代码如下:

public int minPath(int[][] chess) { int row = chess.length; int col = chess[0].length; int[][] dp = new int[row][col]; dp[0][0] = chess[0][0]; for(int i=1; i<row; i++) dp[i][0] = dp[i-1][0] + chess[i][0]; for(int j=1; j<col; j++) dp[0][j] = dp[0][j-1] + chess[0][j]; for(int i=1; i<row; i++) { for(int j=1; j<col; j++) { dp[i][j] = (dp[i-1][j] < dp[i][j-1] ? dp[i-1][j] : dp[i][j-1]) + chess[i][j]; } } return dp[row-1][col-1]; }
观察状态转移方程发现,每次更新(x, y),只需要最多知道上一行即可,没必要知道更早的数据。凡是满足这样条件的动态规划问题,都可以用“滚动数组”的方式做空间上的优化。
使用滚动数组的状态转移方程如上图所示。
代码如下:

public int minPath1(int[][] chess) { int row = chess.length; int col = chess[0].length; int[] dp = new int[col]; dp[0] = chess[0][0]; for(int j=1; j<col; j++) dp[j] = dp[j-1] + chess[0][j]; for(int i=1; i<row; i++) { for(int j=0; j<col; j++) { if(j == 0) dp[j] += chess[i][j]; else dp[j] = (dp[j] < dp[j-1] ? dp[j] : dp[j-1]) + chess[i][j]; } } return dp[col-1]; }
实例三:找零钱问题/0-1背包问题
问题描述。给定某不超过100万元的现金总额,兑换成数量不限的100、50、20、10、5、2、1元的纸币组合,共有多少种组合?
思路:此问题涉及两个类别:面值和总额。所以我们定义dp[i][j]表示使用小于等于i的纸币,凑成j元钱,共有多少种组合方法。比如dp[100][500]表示使用面值不大于100的纸币,凑出500块钱,共有多少种组合方法。
进一步思考,如果面值都是1元的,则无论总额多少,可行的组合数都为1.比如只用1元的纸币凑出100元,显然只有一种组合方法。那么如果多出一种面值呢?组合数有什么变化?
回到dp[100][500],既然用小于等于100的纸币凑出500块钱,则组合中只会要么包含至少一张100块的纸币,要么不包含100块的纸币。所以我们可以分成两种情况考虑:
1)如果没有包括100元,则用到的最大面值可能为50元,即使用面值小于等于50的纸币,凑出500块钱,表示形式为:dp[50][500];
2)如果必须包含100元,怎么计算呢?既然至少包含100元,我们先拿出100块钱,则还需要凑出400块钱即可完成。用小于或等于100元的纸币凑出400块钱,表示形式为dp[100][400];
将两者综合起来为:dp[100][500] = dp[50][500] + dp[100][400];
为了方便表示,我们定义纸币面值为一个数组:dom[] = {1,2,5,10,20,50,100},这样dom[i]和dom[i-1]就表示相邻的纸币面额了。i的意义从面值变成了面值下标。
根据上面分析,对于一般情况,我们有dp[i][j] = dp[i-1][j] + dp[i][j-dom[i]]. ]有了一般情况,在考虑两种特殊情况:
如果dp[i][0]应该返回啥?dp[i][0]表示用小于等于i的纸币,凑出0块钱,我们可以定义这种情况的值为1;
如果dp[0][j]应该返回啥?dp[0][j]表示用小于等于0的纸币,凑出j块钱,我们可以定义这种情况的值为1.
再看dp[100][78],用小于等于100元的纸币凑出78块钱,这时组合中一定不会包含100块的纸币,因此dp[100][78] = dp[50][78],即当j < dom[i]时,dp[i][j] = dp[i-1][j]。
这样整个dp的过程就出来了:

代码为:

public int charge(int[] money, int total) { int row = money.length; int col = total + 1; int[][] dp = new int[row][col]; for(int j=0; j<col; j++) dp[0][j] = 1; //表示用1块钱凑出任何金额的组合数都为1 for(int i=1; i<row; i++) { dp[i][0] = 1; for(int j=1; j<col; j++) { if(j < money[i]) //表示要凑出的金额数小于当前的纸币面额,如dp[100][87] = dp[50][87] dp[i][j] = dp[i-1][j]; else dp[i][j] = dp[i-1][j] + dp[i][j-money[i]]; } } return dp[row-1][col-1]; }
总结,什么时候适合用动态规划呢?
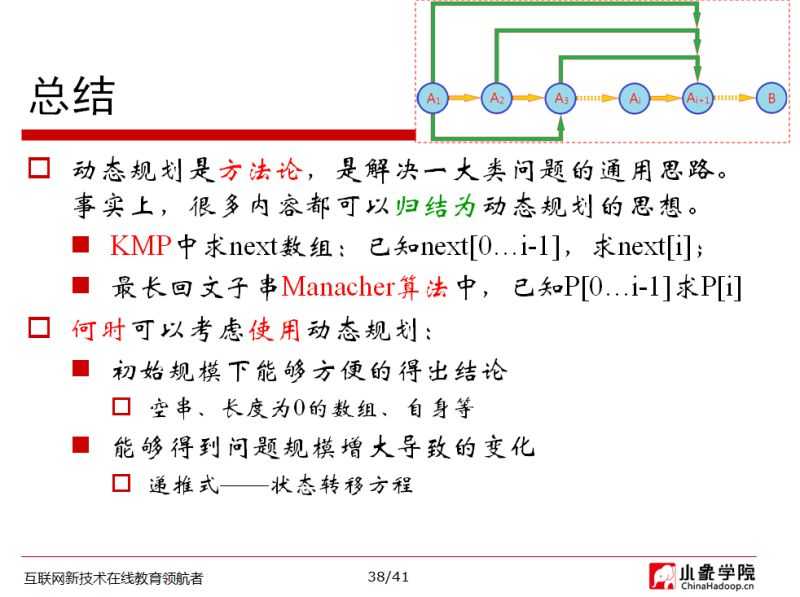
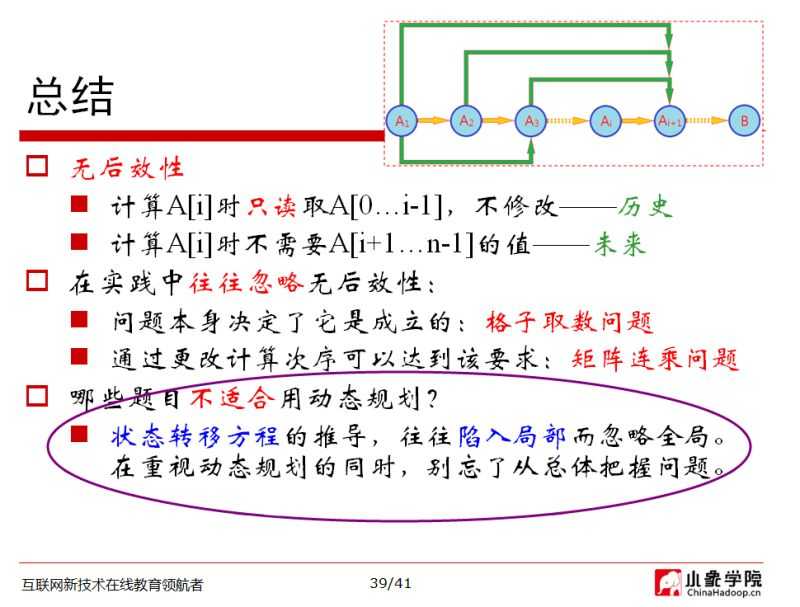
总之,动态规划只是一种解决问题的思路,要灵活运用这种方法,多做练习,就能很快找到灵感了。
标签:
原文地址:http://www.cnblogs.com/little-YTMM/p/5372680.html