堆是实现

标签：堆的实现

#include<iostream>
#include<vector>
#include<assert.h>
#include<math.h>
using namespace std;

template<class T>
class Less
{
public:
    bool operator()(const T& L, const T& R)
    {
        return L < R;
    }
};

template<class T>
class Greater
{
public:
    bool operator()(const T& L, const T& R)
    {
        return L > R;
    }
};

template<class T,class COM>
class Heap
{
public:
    Heap(T* arr,size_t size)
    {
        for (size_t index = 0; index < size; index++)
        {
            _arr.push_back(arr[index]);
        }

        for (int parent = (size - 2) / 2; parent >= 0; --parent)   //找到最后一个非叶子节点  然后逐个调
        {                                                          //注意这里不能用size_t类型 进行（--）时注意size_t的 0 边界
            _AdjustDown(parent,size);
        }
        
    }

    void Print()
    {
        for (size_t index = 0; index < _arr.size(); ++index)
        {
            cout << _arr[index] << "  ";
        }
        cout << endl;
    }

    void Push(const T& num)
    {
        _arr.push_back(num);
        _AdjustUp(_arr.size() - 1);//把加的数据放在最后一个节点
    }

    void Pop()     //只能pop出_arr[0]  
    {
        assert(_arr.size() > 0);
        swap(_arr[0], _arr[_arr.size() - 1]);
        _arr.pop_back();
        /*for (int parent = (_arr.size() - 2) / 2; parent >= 0; --parent)
        {
            _AdjustDown(parent, _arr.size());
        }*/                                                 //不需要再把每个都调整  因为只有根节点变了
        _AdjustDown(0, _arr.size());
    }


protected:
    void _AdjustDown(size_t parent,size_t size)
    {
        while (parent <= size - 1)   //最低到最后一个节点（size - 1）处
        {
            size_t leftchild = parent * 2 + 1;
            if ((leftchild + 1) <= (size - 1) && _com(_arr[leftchild + 1], _arr[leftchild])) //选择两个子孩子中最小的一个
            {
                leftchild++;
            }

            if (leftchild <= (size - 1) && _com(_arr[leftchild], _arr[parent]))   // 使父亲节点最小
            {
                swap(_arr[parent], _arr[leftchild]);
                parent = leftchild;       //如果要交换   则还要调整变了的孩子节点
            }
            else
            {
                break;  //如果不用交换  则调整下一个节点
            }
        }
    }

    void _AdjustUp(int child)
    {
        int parent = (child - 1) / 2;
        while (parent >= 0)
        {
            if (_com(_arr[child], _arr[parent]))
            {
                swap(_arr[parent], _arr[child]);
                child = parent;
                parent = (child - 1) / 2;
            }
            else
            {
                break;
            }
        }
    }
    
protected:
    vector<T> _arr;
    COM _com;
};



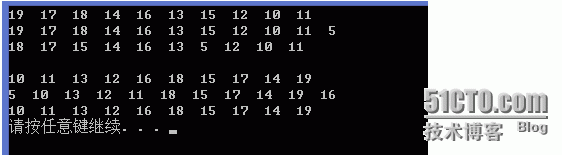
void Test1()
{
    int arr[] = { 10, 16, 18, 12, 11, 13, 15, 17, 14, 19};
    Heap<int,Greater<int>> h1(arr, 10);
    h1.Print();
    h1.Push(5);
    h1.Print();
    h1.Pop();
    h1.Print();
    cout << endl;

    Heap<int, Less<int>> h2(arr, 10);
    h2.Print();
    h2.Push(5);
    h2.Print();
    h2.Pop();
    h2.Print();

}

int main()
{
    Test1();
    return 0;
}

本文出自 “水仙花” 博客，请务必保留此出处http://10704527.blog.51cto.com/10694527/1762367

堆是实现

标签：堆的实现

原文地址：http://10704527.blog.51cto.com/10694527/1762367