数据结构学习笔记05图 (邻接矩阵邻接表-->BFS DFS)

时间：2016-04-10 23:52:13 阅读：707 评论：0 收藏：0 [点我收藏+]

标签：

数据结构之图

图(Graph)

包含
　　一组顶点：通常用V (Vertex) 表示顶点集合
　　一组边：通常用E (Edge) 表示边的集合
　　　　边是顶点对：(v, w) ∈E ，其中v, w ∈ V
　　　　有向边<v, w> 表示从v指向w的边（单行线）
　　　　不考虑重边和自回路

无向图：边是无向边(v, w)

有向图：边是有向边<v, w>

连通：如果从V到W存在一条（无向）路径，则称V和W是连通的

连通图(Connected Graph)：如果对于图的任一两个顶点v、w∈V，v和w都是连通的，则称该图为连通图。图中任意两顶点均连通。

连通分量(Connected Component):无向图中的极大连通子图。

　　极大顶点数：再加1个顶点就不连通了
　　极大边数：包含子图中所有顶点相连的所有边

强连通：有向图中顶点V和W之间存在双向路径，则称V和W是强连通的。
强连通图：有向图中任意两顶点均强连通。
强连通分量：有向图的极大强连通子图。

路径：V到W的路径是一系列顶点{V, v1, v2, …,vn, W}的集合，其中任一对相邻的顶点间都有图中的边。路径的长度是路径中的边数（如果带权，则是所有边的权重和）。

　　　如果V到W之间的所有顶点都不同，则称简单路径
回路：起点等于终点的路径

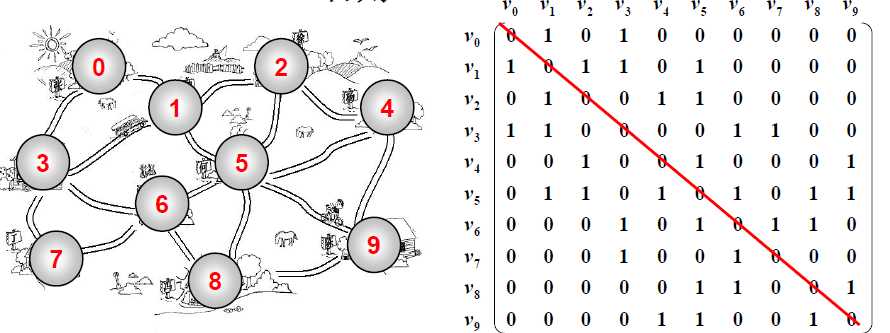
一.邻接矩阵

图的邻接矩阵存储方式就是用一个二维数组来表示。

邻接矩阵G[N][N]——N个顶点从0到N-1编号

顶点i、j有边，则G[i][j] = 1 或边的权重

　　技术分享

邻接矩阵的优点

　　直观、简单、好理解
　　方便检查任意一对顶点间是否存在边
　　方便找任一顶点的所有“邻接点”（有边直接相连的顶点）
　　方便计算任一顶点的“度”（从该点发出的边数为“出度”，指向该点的边数为“入度”）
　　无向图：对应行（或列）非0元素的个数
　　有向图：对应行非0元素的个数是“出度”；对应列非0元素的个数是“入度”

邻接矩阵的缺点

　　浪费空间—— 存稀疏图（点很多而边很少）有大量无效元素
　　　　对稠密图（特别是完全图）还是很合算的
　　　　浪费时间—— 统计稀疏图中一共有多少条边

  1 /* 图的邻接矩阵表示法 */
  2 #include <iostream>
  3 #include <cstdio>
  4 #include <cstdlib> 
  5 #include <queue>
  6 using namespace std;
  7 
  8 #define MaxVertexNum 100    /* 最大顶点数设为100 */
  9 #define INFINITY 65535        /* 设为双字节无符号正数的最大值65535*/
 10 typedef int Vertex;         /* 用顶点下标表示顶点,为整型 */
 11 typedef int WeightType;        /* 边的权值设为整型 */
 12 typedef char DataType;        /* 顶点存储的数据类型设为字符型 */
 13   
 14 /* 边的定义 */
 15 typedef struct ENode *PtrToENode;
 16 struct ENode{
 17     Vertex V1, V2;      /* 有向边<V1, V2> */
 18     WeightType Weight;  /* 权重 */
 19 };
 20 typedef PtrToENode Edge;
 21          
 22 /* 图结点的定义 */
 23 typedef struct GNode *PtrToGNode;
 24 struct GNode{
 25     int Nv;  /* 顶点数 */
 26     int Ne;  /* 边数   */
 27     WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
 28     DataType Data[MaxVertexNum];      /* 存顶点的数据 */
 29     /* 注意：很多情况下，顶点无数据，此时Data[]可以不用出现 */
 30 };
 31 typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */
 32 bool Visited[MaxVertexNum] = {false};
 33 
 34 MGraph CreateGraph( int VertexNum );
 35 void InsertEdge( MGraph Graph, Edge E );
 36 MGraph BuildGraph();
 37 bool IsEdge( MGraph Graph, Vertex V, Vertex W );
 38 void InitVisited();
 39 Vertex BFS ( MGraph Graph, Vertex S, void (*Visit)(Vertex) );
 40 Vertex DFS ( MGraph Graph, Vertex S, void (*Visit)(Vertex) );
 41 Vertex listDFS( MGraph Graph, void (*Visit)(Vertex) );
 42 
 43 MGraph CreateGraph( int VertexNum )
 44 { /* 初始化一个有VertexNum个顶点但没有边的图 */
 45     Vertex V, W;
 46     MGraph Graph;
 47       
 48     Graph = (MGraph)malloc(sizeof(struct GNode)); /* 建立图 */
 49     Graph->Nv = VertexNum;
 50     Graph->Ne = 0;
 51     /* 初始化邻接矩阵 */
 52     /* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
 53     for (V=0; V<Graph->Nv; V++)
 54         for (W=0; W<Graph->Nv; W++)  
 55             Graph->G[V][W] = INFINITY;
 56               
 57     return Graph; 
 58 }
 59          
 60 void InsertEdge( MGraph Graph, Edge E )
 61 {
 62      /* 插入边 <V1, V2> */
 63      Graph->G[E->V1][E->V2] = E->Weight;    
 64      /* 若是无向图，还要插入边<V2, V1> */
 65      Graph->G[E->V2][E->V1] = E->Weight;
 66 }
 67   
 68 MGraph BuildGraph()
 69 {
 70     MGraph Graph;
 71     Edge E;
 72     Vertex V;
 73     int Nv, i;
 74       
 75     scanf("%d", &Nv);   /* 读入顶点个数 */
 76     Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */ 
 77       
 78     scanf("%d", &(Graph->Ne));   /* 读入边数 */
 79     if ( Graph->Ne != 0 ) { /* 如果有边 */ 
 80         E = (Edge)malloc(sizeof(struct ENode)); /* 建立边结点 */ 
 81         /* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */
 82         for (i=0; i<Graph->Ne; i++) {
 83             scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); 
 84             /* 注意：如果权重不是整型，Weight的读入格式要改 */
 85             InsertEdge( Graph, E );
 86         }
 87     } 
 88   
 89     /* 如果顶点有数据的话，读入数据 */
 90     for (V=0; V<Graph->Nv; V++) 
 91         scanf(" %c", &(Graph->Data[V]));
 92   
 93     return Graph;
 94 }
 95 /* 邻接矩阵存储的图 - BFS */
 96   
 97 /* IsEdge(Graph, V, W)检查<V, W>是否图Graph中的一条边，即W是否V的邻接点。  */
 98 /* 此函数根据图的不同类型要做不同的实现，关键取决于对不存在的边的表示方法。*/
 99 /* 例如对有权图, 如果不存在的边被初始化为INFINITY, 则函数实现如下:         */
100 bool IsEdge( MGraph Graph, Vertex V, Vertex W )
101 {
102     return Graph->G[V][W]<INFINITY ? true : false;
103 }
104 
105 //初始化 Visited[] = false
106 void InitVisited()
107 {
108     for(int i = 0; i < MaxVertexNum; i++)
109         Visited[i] = false;
110 } 
111 
112 void Visit(Vertex v)
113 {
114     printf("%d ",v);
115 }
116 
117 /* Visited[]为全局变量，已经初始化为false */
118 Vertex BFS ( MGraph Graph, Vertex S, void (*Visit)(Vertex) )
119 {   /* 以S为出发点对邻接矩阵存储的图Graph进行BFS搜索 */
120     queue<Vertex> Q;     
121     Vertex V, W;
122   
123     /* 访问顶点S：此处可根据具体访问需要改写 */
124     Visit( S );
125     Visited[S] = true; /* 标记S已访问 */
126     Q.push(S); /* S入队列 */
127       
128     while ( !Q.empty() ) {
129         V = Q.front();
130         Q.pop();      /* 弹出V */
131         for( W=0; W < Graph->Nv; W++ ) /* 对图中的每个顶点W */
132             /* 若W是V的邻接点并且未访问过 */
133             if ( !Visited[W] && IsEdge(Graph, V, W) ) {
134                 /* 访问顶点W */
135                 Visit( W );
136                 Visited[W] = true; /* 标记W已访问 */
137                 Q.push(W); /* W入队列 */
138             }
139     } /* while结束*/
140     printf("\n");
141     
142     //遍历 Visited[]列出所有BFS的顶点 若只需一个顶点开始的BFS可忽略 
143     Vertex i;
144     for(i = 0; i < Graph->Nv; i++) {
145         if(Visited[i] == false)//找出未被访问过的结点记录i值 
146             break;
147     }
148     if(i == Graph->Nv)
149         return 0;
150     else
151         return BFS(Graph,i,Visit);
152 }
153 
154 /* 以S为出发点对邻接矩阵存储的图Graph进行DFS搜索 */
155 Vertex DFS ( MGraph Graph, Vertex S, void (*Visit)(Vertex) )
156 {
157     Visited[S] = true;
158     Visit(S);
159     for(Vertex w = 0; w < Graph->Nv; w++) {
160         if( IsEdge(Graph, S, w) && Visited[w]==false) {
161             DFS(Graph,w,Visit);
162         }
163     }    
164 }
165 //列出DFS的所有顶点 
166 Vertex listDFS( MGraph Graph, void (*Visit)(Vertex) )
167 {
168     Vertex i;
169     for(i = 0; i < Graph->Nv; i++) {
170         if(Visited[i] == false)//找出未被访问过的结点记录i值 
171             break;
172     }
173     if(i == Graph->Nv)
174         return 0;
175     DFS(Graph, i, Visit);
176     printf("\n");
177     
178     return listDFS(Graph,Visit);
179 }
180 int main()
181 {
182     MGraph graph;
183     graph = BuildGraph();
184     InitVisited(); 
185     listDFS(graph,&Visit);
186     InitVisited(); 
187     BFS(graph,0,&Visit);
188     return 0;
189 }

sj5_0 图的邻接矩阵

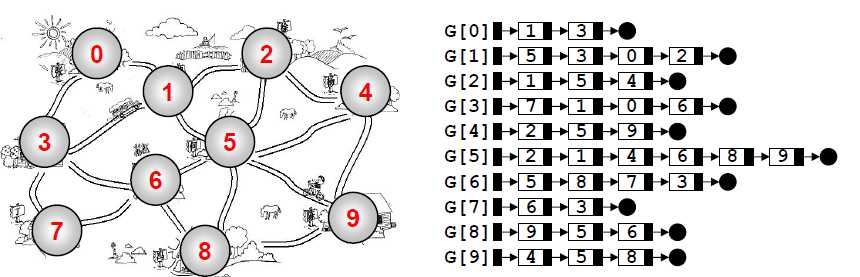
二.邻接表

G[N]为指针数组，对应矩阵每行一个链表，只存非0元素。

技术分享

邻接表的优点
　　方便找任一顶点的所有“邻接点”
　　节约稀疏图的空间
　　需要N个头指针+ 2E个结点（每个结点至少2个域）
　　方便计算任一顶点的“度”？
　　　　对无向图：是的
　　　　对有向图：只能计算“出度”；需要构造“逆邻接表”（存指向自己的边）来方便计算“入度”

邻接表的缺点

　　不方便检查任意一对顶点间是否存在边

  1 /* 图的邻接表表示法 */ 
  2 //build用的 头插法 尾插法遍历 出来不同 但无影响 
  3 #include <iostream>
  4 #include <cstdio>
  5 #include <cstdlib> 
  6 #include <queue>
  7 using namespace std;
  8 
  9 #define MaxVertexNum 100    /* 最大顶点数设为100 */
 10 typedef int Vertex;         /* 用顶点下标表示顶点,为整型 */
 11 typedef int WeightType;        /* 边的权值设为整型 */
 12 typedef char DataType;        /* 顶点存储的数据类型设为字符型 */
 13   
 14 /* 边的定义 */
 15 typedef struct ENode *PtrToENode;
 16 struct ENode{
 17     Vertex V1, V2;      /* 有向边<V1, V2> */
 18     WeightType Weight;  /* 权重 */
 19 };
 20 typedef PtrToENode Edge;
 21   
 22 /* 邻接点的定义 */
 23 typedef struct AdjVNode *PtrToAdjVNode; 
 24 struct AdjVNode{
 25     Vertex AdjV;        /* 邻接点下标 */
 26     WeightType Weight;  /* 边权重 */
 27     PtrToAdjVNode Next;    /* 指向下一个邻接点的指针 */
 28 };
 29   
 30 /* 顶点表头结点的定义 */
 31 typedef struct Vnode{
 32     PtrToAdjVNode FirstEdge;/* 边表头指针 */
 33     DataType Data;            /* 存顶点的数据 */
 34     /* 注意：很多情况下，顶点无数据，此时Data可以不用出现 */
 35 } AdjList[MaxVertexNum];    /* AdjList是邻接表类型 */
 36   
 37 /* 图结点的定义 */
 38 typedef struct GNode *PtrToGNode;
 39 struct GNode{  
 40     int Nv;     /* 顶点数 */
 41     int Ne;     /* 边数   */
 42     AdjList G;  /* 邻接表 */
 43 };
 44 typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */
 45 bool Visited[MaxVertexNum] = {false}; 
 46 
 47 LGraph CreateGraph( int VertexNum );
 48 void InsertEdge( LGraph Graph, Edge E );
 49 LGraph BuildGraph();
 50 void Visit( Vertex V );
 51 void InitVisited();
 52 void DFS( LGraph Graph, Vertex V, void (*Visit)(Vertex) );
 53 Vertex listDFS( LGraph Graph, void (*Visit)(Vertex) );
 54 int BFS( LGraph Graph, Vertex V, void (*Visit)(Vertex) );
 55 
 56 LGraph CreateGraph( int VertexNum )
 57 { /* 初始化一个有VertexNum个顶点但没有边的图 */
 58     Vertex V;
 59     LGraph Graph;
 60       
 61     Graph = (LGraph)malloc( sizeof(struct GNode) ); /* 建立图 */
 62     Graph->Nv = VertexNum;
 63     Graph->Ne = 0;
 64     /* 初始化邻接表头指针 */
 65     /* 注意：这里默认顶点编号从0开始，到(Graph->Nv - 1) */
 66        for (V=0; V<Graph->Nv; V++)
 67         Graph->G[V].FirstEdge = NULL;
 68               
 69     return Graph; 
 70 }
 71          
 72 void InsertEdge( LGraph Graph, Edge E )
 73 {
 74     PtrToAdjVNode NewNode;
 75       
 76     /* 插入边 <V1, V2> */
 77     /* 为V2建立新的邻接点 */
 78     NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
 79     NewNode->AdjV = E->V2;
 80     NewNode->Weight = E->Weight;
 81     /* 将V2插入V1的表头 */
 82     NewNode->Next = Graph->G[E->V1].FirstEdge;
 83     Graph->G[E->V1].FirstEdge = NewNode;
 84           
 85     /* 若是无向图，还要插入边 <V2, V1> */
 86     /* 为V1建立新的邻接点 */
 87     NewNode = (PtrToAdjVNode)malloc(sizeof(struct AdjVNode));
 88     NewNode->AdjV = E->V1;
 89     NewNode->Weight = E->Weight;
 90     /* 将V1插入V2的表头 */
 91     NewNode->Next = Graph->G[E->V2].FirstEdge;
 92     Graph->G[E->V2].FirstEdge = NewNode;
 93 }
 94   
 95 LGraph BuildGraph()
 96 {
 97     LGraph Graph;
 98     Edge E;
 99     Vertex V;
100     int Nv, i;
101       
102     scanf("%d", &Nv);   /* 读入顶点个数 */
103     Graph = CreateGraph(Nv); /* 初始化有Nv个顶点但没有边的图 */ 
104       
105     scanf("%d", &(Graph->Ne));   /* 读入边数 */
106     if ( Graph->Ne != 0 ) { /* 如果有边 */ 
107         E = (Edge)malloc( sizeof(struct ENode) ); /* 建立边结点 */ 
108         /* 读入边，格式为"起点 终点 权重"，插入邻接矩阵 */
109         for (i=0; i<Graph->Ne; i++) {
110             scanf("%d %d %d", &E->V1, &E->V2, &E->Weight); 
111             /* 注意：如果权重不是整型，Weight的读入格式要改 */
112             InsertEdge( Graph, E );
113         }
114     } 
115   
116     /* 如果顶点有数据的话，读入数据 */
117     for (V=0; V<Graph->Nv; V++) 
118         scanf(" %c", &(Graph->G[V].Data));
119   
120     return Graph;
121 }
122 
123 void Visit( Vertex V )
124 {
125     printf("%d ", V);
126 }
127 
128 //初始化 Visited[] = false
129 void InitVisited()
130 {
131     for(int i = 0; i < MaxVertexNum; i++)
132         Visited[i] = false;
133 }  
134 
135 /* Visited[]为全局变量，已经初始化为false */
136 void DFS( LGraph Graph, Vertex V, void (*Visit)(Vertex) )
137 {   /* 以V为出发点对邻接表存储的图Graph进行DFS搜索 */
138     PtrToAdjVNode W;
139       
140     Visit( V ); /* 访问第V个顶点 */
141     Visited[V] = true; /* 标记V已访问 */
142   
143     for( W=Graph->G[V].FirstEdge; W; W=W->Next ) /* 对V的每个邻接点W->AdjV */
144         if ( !Visited[W->AdjV] )    /* 若W->AdjV未被访问 */
145             DFS( Graph, W->AdjV, Visit );    /* 则递归访问之 */
146 }
147 Vertex listDFS( LGraph Graph, void (*Visit)(Vertex) )
148 {
149     Vertex i;
150     for(i = 0; i < Graph->Nv; i++) {
151         if(Visited[i] == false)//找出未被访问过的结点记录i值 
152             break;
153     }
154     if(i == Graph->Nv)
155         return 0;
156     DFS(Graph, i, Visit);
157     printf("\n");
158     return listDFS(Graph,Visit);
159 } 
160 
161 int BFS( LGraph Graph, Vertex V, void (*Visit)(Vertex) )
162 {
163     queue<Vertex> Q;     
164     Vertex W;
165     
166     Visit( V ); /* 访问第V个顶点 */
167     Visited[V] = true; /* 标记V已访问 */
168     Q.push(V);
169     
170     while( !Q.empty() ) {
171         W = Q.front();
172         Q.pop();
173         for(PtrToAdjVNode tempV = Graph->G[W].FirstEdge; tempV; tempV=tempV->Next ) /* 对W的每个邻接点tempV->AdjV */
174             if( !Visited[tempV->AdjV]) {
175                 Visited[tempV->AdjV] = true;
176                 Visit(tempV->AdjV);
177                 Q.push(tempV->AdjV);
178             }
179     }
180     printf("\n");
181     
182     //遍历 Visited[]列出所有BFS的顶点 若只需一个顶点开始的BFS可忽略 
183     Vertex i;
184     for(i = 0; i < Graph->Nv; i++) {
185         if(Visited[i] == false)//找出未被访问过的结点记录i值 
186             break;
187     }
188     if(i == Graph->Nv)
189         return 0;
190     else
191         return BFS(Graph,i,Visit);
192 }
193 
194 
195 int main()
196 {
197     LGraph graph;
198     graph = BuildGraph();
199     InitVisited();
200     listDFS(graph,&Visit);
201     InitVisited();
202     BFS(graph, 0, &Visit);
203     return 0;
204 }