栈的一些小小应用

标签：include   表达式   优先级   程序   栈的应用   迷宫   

昨天刚实现了栈的一些基本操作，今天就来实现一点栈的应用把！

首先，写一点比较简单的：

1.逆波兰表达式的计算。

    在通常的表达式中，二元运算符总是置于与之相关的两个运算对象之间，这种表示法也称为中缀表示。逆波兰表达式也称为后缀表达式。比如：

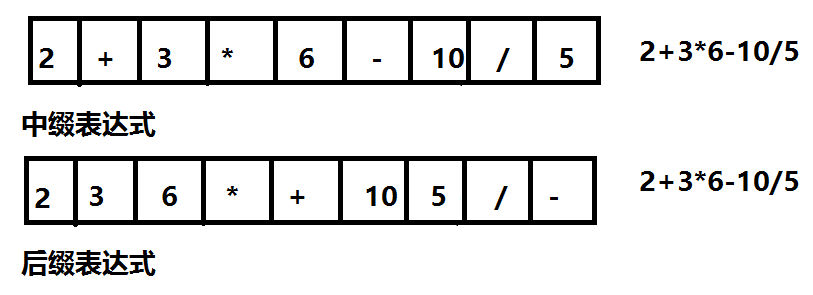    两种表达式如果在程序中运行时，后缀表达式不需要考虑符号优先级的问题。

现在通过一个程序去计算一个简单的后缀表达式：

#pragma once

#include <iostream>
#include <assert.h>
#include <stack>
using namespace std;

enum Type
{
	OP_NUM,//数字
	OP_SYMBOL,//运算符
};

enum SYMBOL
{
	ADD,
	SUB,
	MUL,
	DIV,
};

struct Cell
{
	Type _type;//类型（1.数字 2.运算符）
	int _value;
};

int CountSymbol(Cell a[], size_t size)
{
	assert(a);
	stack<int> s;

	for (size_t i = 0; i < size; i++)//依次读取每个数据
	{
		if (a[i]._type == OP_NUM)
		{
			s.push(a[i]._value);
		}
		else
		{
			//取出运算符前面的两个数字进行计算
			int right = s.top();
			s.pop();//栈的特性，只能pop一个后去下一个数
			int left = s.top();
			s.pop();

			switch (a[i]._value)
			{
				//把计算结果压入栈中
			case ADD:
				s.push(left + right);
				break;
			case SUB:
				s.push(left - right);
				break;
			case MUL:
				s.push(left * right);
				break;
			case DIV:
				s.push(left / right);
				break;
			}
		}
	}
	return s.top();
}

void TestSymbol()
{
	//12*(3+4)-6+8/2 = 82
	//12 3 4 + * 6 - 8 2 / +   逆波兰表达式
	Cell a[] =
	{
		{OP_NUM,12},
		{OP_NUM, 3},
		{OP_NUM,4},
		{OP_SYMBOL,ADD},
		{OP_SYMBOL,MUL},
		{OP_NUM,6},
		{OP_SYMBOL,SUB},
		{OP_NUM,8},
		{OP_NUM,2},
		{OP_SYMBOL,DIV},
		{OP_SYMBOL,ADD},
	};
	int ret = CountSymbol(a, sizeof(a) / sizeof(a[0]));
	cout << "ret=" << ret << endl;
}

在这个程序中可以看到应用了栈的一个重要特性，“后进先出”。

2.迷宫是一个很长久的话题，今天我就用代码来实现它。

迷宫问题有一个很重要的点，就是“回溯”，顾名思义，就是沿着走过的路依次往回走。

为了简单起见，直接写一个迷宫，定义为“Maze.txt”文件

                              （0表示通路，1表示墙）

本文出自 “不断进步的空间” 博客，请务必保留此出处http://10824050.blog.51cto.com/10814050/1762816

栈的一些小小应用

标签：include   表达式   优先级   程序   栈的应用   迷宫   

原文地址：http://10824050.blog.51cto.com/10814050/1762816