标签:
对于分类数据的分析,最简单也是最广泛使用的是卡方检验,但卡方检验在处理分类数据时,有两个局限:
1.卡方检验只能简单描述变量间的相关关系,而无法分析出具体的因果关系或变量间相互作用(效应)大小
2.卡方检验通常用于2*2列联表,而对于高维列联表,则无法系统的评价变量间的关系,而对数线性模型则是分析高维列联表的常用方法。
基于以上问题,我们除了可以使用Logistic模型之外,还可以使用对数线性模型进行分析。
对数线性模型的结构类似于方差分析,思想也和方差分析一样,不同的是方差分析用于连续变量,而对数线性模型用于分类变量。在方差分析中,观测值y的变异由各因素的主效应、各因素之间的交互效应、随机误差三者之和组成。而对于分类变量也可以采用这种方法进行分解,只不过此时的观测值y为频数而不是实际的观测值,最终观测值变异的组成也不是相加关系,而是乘积关系。以两个分类变量α、β为例:
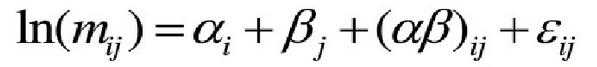
Mij代表第i行第j列的频数
αi代表变量α的主效应
βj代表变量β的主效应
(αβ)ij代表变量αβ的交互作用
εij代表随机误差
分类数据的频数分布一般分为多项式分布、二项式分布、泊松分布,取值在0—+∞之间,因此等式两边都取其对数ln,这样可以使期望频数取值在-∞—+∞,这就是所谓的对数线性模型。
模型的独立参数和自由度:
独立参数个数=分类数-限制条件数
数据提供的信息量=列联表中网格的数量
模型自由度=信息量-独立参数个数
对数线性模型的一个假设前提是:每个分类变量各水平的效应之和等于0
=============================================
对数线性模型的统计检验:
对数线性模型的假设检验都是基于Pearson卡方检验和似然比卡方检验L2,当样本规模较大时,这两个统计值很接近,但似然比卡方更加稳健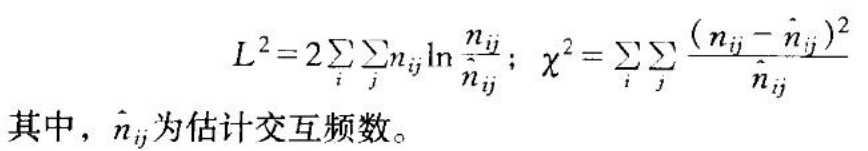
1.对模型的整体检验
也就是拟合优度检验,两种卡方的零假设是:检验模型的频数估计与观测频数无差异,也就是拟合度良好
2.分层效应检验
类似于逐步回归的筛选自变量,分层效应检验就是逐步筛选交互作用,每剔除一种交互作用,就检验一次,主要是:某一阶及更高阶所有交互作用项的集体检验,检验是否显著表明这一阶及更高阶中是否至少有一项分类的效应是有意义的。
3.单项效应检验
可视为分层效应检验的进一步分解,分层效应检验只能说明至少有一项效应是有意义的,但是具体是哪些分类的效应有意义并没有说明,因此需要做单项效应检验。
4.单个参数估计检验
检验出某一分类效应有意义之后,还需具体到检验这一分类的哪些水平有意义。
=======================================
与Logit模型的关系
对数线性模型和Logit模型都是分类数据的分析方法,当因变量为二分类变量时,二者是等价的,而且SPSS软件对数线性模型中就有logit菜单,那么二者有哪些区别,又该如果选择呢?
1.首先,对数线性模型主要是针对变量间的交互作用进行分析,不区分自变量与因变量,也不分析非因果关系,Logit模型主要是分析变量间的因果关系,在交互作用分析上则非常繁琐,要涉及很多哑变量
2.其次,对数线性模型要求变量都为分类变量,如果是连续型变量要离散化,这会损失数据信息,而Logit模型自变量可以是分类变量或连续变量。
3.再者,对数线性模型的计算基础是频数,因此对样本有一定要求,一般认为样本量至少应为列联表格子数的4-5倍,且80%以上的格子频数大于5。而Logit模型对此并无过多要求,但这并不是说我们可以忽略样本量这个因素,统计学的任何分析检验都是样本量越大越好。
没有任何一种分析方法是一蹴而就的,在实际分析中,我们应该综合各种分析方法的优缺点,扬长避短,比如,对数线性模型在变量或变量水平较多的情况下,不饱和模型过多,比较复杂,我们可以先用对数线性模型分析主效应和交互效应,剔除一部分没有统计学意义的变量和水平,将数据简化之和再做Logistic回归。
标签:
原文地址:http://www.cnblogs.com/xmdata-analysis/p/5386998.html