标签:
强连通分量是有向图中的概念,就是每一个顶点到其它点都由路径,注意有方向.
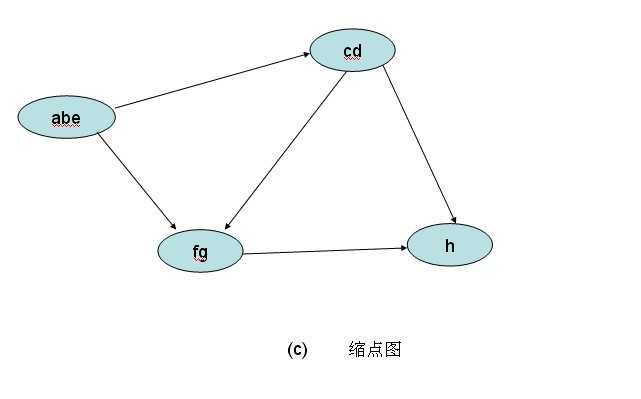
有向图强连通分量:在有向图G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量。
Kosaraju_Algorithm:
1 #include <iostream> 2 #include <cstring> 3 #include <vector> 4 using namespace std; 5 const int MAX = 105;/****** * v为原图 * rv为所有边逆向后的新图 * s记录第一遍dfs后各点的结束时间:最晚结束的在栈顶 ******/ 6 vector<int> v[MAX], rv[MAX], s;/****** * num[v]点v所属连通分量的编号 * tree_n[i]第i个连通分量内点的个数 ******/ 7 int num[MAX], tree_n[MAX], cnt; 8 bool mark[MAX],ml[MAX]; 9 void dfs_1(int x)//第一步计算dfs结束时间,将时间由小到大对应的数入s 10 { 11 mark[x] = 1; 12 for (int i = 0; i < v[x].size(); ++i) 13 { 14 if (!mark[v[x][i]]) 15 { 16 dfs_1(v[x][i]); 17 } 18 } 19 s.push_back(x); 20 } 21 22 void dfs_2(int x)//从s的尾取数再rv中dfs 23 { 24 num[x] = cnt; //点v所属连通分量的编号为cnt 25 ++tree_n[cnt]; //记录编号为cnt的连通分量中的元数个数 26 mark[x] = 1; 27 for (int i = 0; i < rv[x].size(); ++i) 28 { 29 if (!mark[rv[x][i]]) 30 { 31 dfs_2(rv[x][i]); 32 } 33 } 34 } 35 void cal(int n) 36 { 37 int i,j; 38 memset(mark, 0, sizeof(mark)); 39 memset(ml,0,sizeof(ml)); 40 for (i = 1; i <= n; ++i) 41 { 42 for (j = 0; j < v[i].size(); ++j) 43 { 44 int x = v[i][j]; 45 if (num[i] != num[x])//检查强连通分量是否有出度,有就对应的mark[i]=1 46 { 47 mark[num[x]] = 1; 48 ml[num[i]]=1; 49 } 50 } 51 } 52 int flag = 0,flg =0, ans; 53 for (i = 1; i <= cnt; ++i) //检查有几个强连通分量的入度为0 54 { 55 if (!mark[i]) 56 { 57 ans = i; 58 ++flag; 59 } 60 if (!ml[i]) 61 { 62 ++flg; 63 } 64 } 65 cout<<flag<<endl; 66 if(cnt!=1) 67 { 68 flg=flag>flg? flag:flg; 69 cout<<flg<<endl; 70 } 71 else cout<<0<<endl; 72 } 73 74 int main() 75 { 76 77 int a, b, n, i, j; 78 scanf("%d",&n); 79 for(i=1;i<=n;i++) 80 { 81 while(cin>>a&&a) 82 { 83 v[i].push_back(a); 84 rv[a].push_back(i); 85 } 86 87 } 88 89 for (i = 1; i <= n; ++i) 90 { 91 if (!mark[i]) 92 { 93 dfs_1(i); 94 } 95 } 96 memset(mark, 0, sizeof(mark)); 97 memset(tree_n, 0, sizeof(tree_n)); 98 cnt = 0; //cnt记录连通分量的个数 99 for (i = s.size() - 1; i >= 0; --i) 100 { 101 if (!mark[s[i]]) 102 { 103 ++cnt; 104 dfs_2(s[i]); 105 } 106 } 107 cal(n); 108 return 0; 109 }
标签:
原文地址:http://www.cnblogs.com/bytebull/p/5390101.html