标签:
在二维坐标系中,一个位置向量的旋转公式可以由三角函数的几何意义推出.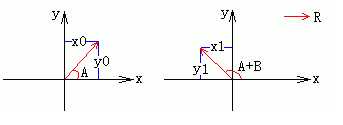
比如上图所示是位置向量R逆时针旋转角度B前后的情况.
在左图中,我们有关系:
x0 = |R| * cosA => cosA = x0 / |R|
y0 = |R| * sinA => sinA = y0 / |R|
在右图中,我们有关系:
x1 = |R| * cos(A+B)
y1 = |R| * sin(A+B)
其中(x1,y1)就是(x0,y0)旋转角B后得到的点,也就是位置向量R最后指向的点.我们展开cos(A+B)和sin(A+B),得到:
x1 = |R| * (cosAcosB - sinAsinB)
y1 = |R| * (sinAcosB + cosAsinB)
现在把 cosA = x0 / |R| 和 sinA = y0 / |R| 代入上面的式子,得到:
x1 = |R| * (x0 * cosB / |R| - y0 * sinB / |R|) => x1 = x0 * cosB - y0 * sinB
y1 = |R| * (y0 * cosB / |R| + x0 * sinB / |R|) => y1 = x0 * sinB + y0 * cosB
这样我们就得到了二维坐标下向量围绕圆点的逆时针旋转公式.顺时针旋转就把角度变为负:
x1 = x0 * cos(-B) - y0 * sin(-B) => x1 = x0 * cosB + y0 * sinB
y1 = x0 * sin(-B) + y0 * cos(-B)=> y1 = -x0 * sinB + y0 * cosB
现在我要把这个旋转公式写成矩阵的形式,有一个概念我简单提一下,平面或空间里的每个线性变换(这里就是旋转变换)都对应一个矩阵,叫做变换矩阵.对一个点实施线性变换就是通过乘上该线性变换的矩阵完成的.好了,打住,不然就跑题了.
所以二维旋转变换矩阵就是:
[cosA sinA] [cosA -sinA]
[-sinA cosA] 或者 [sinA cosA]
我们对向量进行旋转变换可以通过矩阵完成,比如我要向量(x,y)绕原点逆时针旋转角度A:
[x,y] x [cosA sinA] = [x*cosA-y*sinA x*sinA+y*cosA]
[-sinA cosA]
旋转后的向量为:[x*cosA-y*sinA x*sinA+y*cosA]
原文:http://www.zybang.com/question/143ceaa20d3942f3c6dbe9415dd81d0a.html
标签:
原文地址:http://www.cnblogs.com/bofengyu/p/5394969.html