NYOJ 743

标签：

描述

for(i=1;i<=n;i++)

  for(j=i+1;j<=n;j++)

    for(k=j+1;k<=n;k++)

        operation;

你知道 operation 共执行了多少次吗；

输入

输入 m 和n 表示m为for循环的层数，n为for中的n。
(n,m<=2000),输入以n==0和m==0结束

输出

输出operation执行的次数（输入结果mod 1009）

样例输入

2 3
1 3
2 4
0 0

样例输出

3
3
6

　　仔细观察就会发现，这里面的 i, j, k,... 等等，他们的开头处的取值完全不一样，这就好比有n个数值，开头取一个，有n中取法；再取第二个，有n-1中取法；再取第三个，有n-2种取法；。。。一直到再取第m个有n-m+1中取法。这么一说，想到了什么？组合数！有木有！！！就是这么神奇，其实整个题目就是要计算组合数的一个题。

     接着就是组合数公式的编程，而常识告诉我们，一旦计算C(2000,1000)这种情况，用阶层计算是十分恐怖的，辛好结果是要求对1009取余的结果，那么问题来了，如何不用阶层来快速计算组合数。

首先我们回顾下组合数的公式：

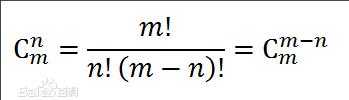
以及组合数的一些性质：

C(n,m)=  C(n-1,m-1)+C(n-1,m)  关于这个公式的证明，可以套用上面的公式来直接证明，还有直接逻辑思考套用到某个实际事例中就能证明，这里就不总结了。

C(n,m)= C(n,m-1) + C(n-1,m-1)  

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 using namespace std;
 5 const int N = 1009;
 6 int f[2005][2005] = {0};
 7 void fun()
 8 {
 9     for(int i = 1; i <= 2000; i++)
10         for(int j = i; j <= 2000; j++)
11         {
12             if(i == j)
13             {
14                 f[i][j] = 1;
15                 continue;
16             }
17             if(i == 1)
18             {
19                 f[i][j] = j%N;
20                 continue;
21             }
22             f[i][j] = ((f[i][j-1]) + (f[i-1][j-1]))%N;
23         }
24 }
25 int main()
26 {
27     fun();
28     int n,m;
29     while(scanf("%d%d",&m,&n),n+m)
30     {
31         printf("%d\n",f[m][n]);
32     }
33     return 0;
34 }

其实这是一个很普遍的问题，就是组合数取模问题，这下就一次性解决了吧。

http://blog.csdn.net/acdreamers/article/details/8037918

http://www.3773.com.cn/NCRE/434536.shtml

NYOJ 743

标签：

原文地址：http://www.cnblogs.com/liugl7/p/5399352.html