标签:
引言:深度学习的浪潮开始于Hinton 的一篇文章 Reducing the Dimensionality of Data with Neural Networks;
代表人物:Geoffery Hinton 链接 :http://www.cs.toronto.edu/~hinton/
Yann LeCun 链接:http://yann.lecun.com/ex/index.html
Yoshua Bengio 链接:http://www.iro.umontreal.ca/~bengioy/yoshua_en/
Andrew Ng 链接:http://www.andrewng.org/
发展历程:
-Hopfield network
–Boltzman machine
–Restricted Boltzman machine
–CNN
–RNN
–LSTM
–Autoencoder
–DBN
–DBM
–Deep Learning
1.CNN
1998年,Yann LeCun设计了一个处理图像的卷积神经网络,并用于文本识别,取得了不错的效果。
目的是要对自然图像,希望直接从图像底层开始进行学习(非结构化特征学习)。即,对于图像识别任务,不必事先提取出人为设计的特征,比如Gabor纹理特征、多尺度小波特征、SIFT特征、HOG特征,等等。(因为这些人为设计的特征有缺点:这些特征具有一些参数,如尺度、梯度方向、频域划分等,其泛化能力不强)
CNN重新设计了多层神经网络的结构(并未改变神经元),原因是如果以图像直接作为输入,并将每个像素看成一个结点,对于200*200大小的图像,则仅输入层就有4万个结点;如果第一隐含层仅仅只包含1000个结点,则权重数量将达到4千万。这显然是一个巨大的计算负担。
为了解决这个问题,CNN采取了三个策略:第一个局部链接,第二个权值共享,第三个下采样(第三个又叫pooling)。
第一个局部链接:每个神经元其实没有必要对全局图像进行感知,只需要对局部进行感知。
第二个权值共享:从图像任何一个局部区域内连接到同一类型的隐含结点,其权重保持不变。
用图像卷积的思想描述上述两个过程就是:使用一个滤波器对图像进行卷积,滤波器的大小和取值并不随区域位置改变,而滤波器的卷积核的权重就是输入层到隐含层的权重。具体如下图所示:
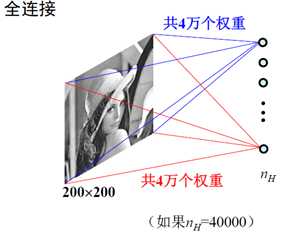

我们大大的减少了需要学习的权重的数量,然后我们就有能力多加几个滤波器了:
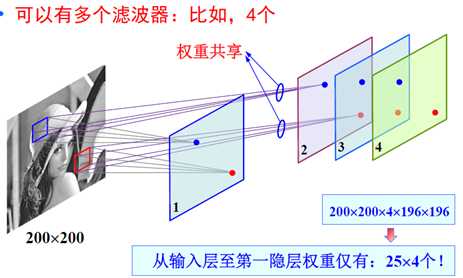
这样做之后,隐含层的节点数不是随便选的,而是由原图像的大小,滤波器的大小,滤波器的个数共同决定的。维度较高,容易产生过拟合,所以引进了第三个策略,pooling——对不同位置的特征进行聚合统计,比如,计算图像一个区域上的某个特定特征的平均值(或最大值)

接下来是第一隐层到第二隐层的操作,要注意,是对第一层中多个滤波器的结果进行同时加权处理(也就是用一个立方体滤波器进行下一次滤波),当然局部连接和权值共享还是同样的方式,只不过是相当于作用在4幅图像上了:
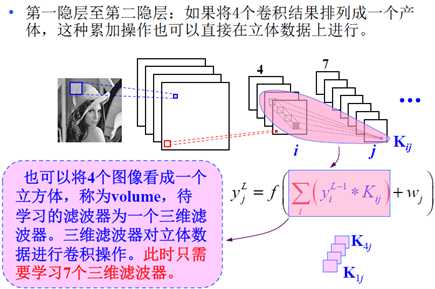
接下来的每一层都进行相同的操作(但是卷积核的尺寸与个数是不同的):
–卷积 (Convolution)
•将卷积之和加到下一层
•对卷积之和进行激励 (特别指出:也可以在pooling之后求激励)
–聚合 (Pooling)
•下采样,两种基本的运算:
–2*2窗口取平均(或取最大值)
在最后两层加入全连接的多层感知器:
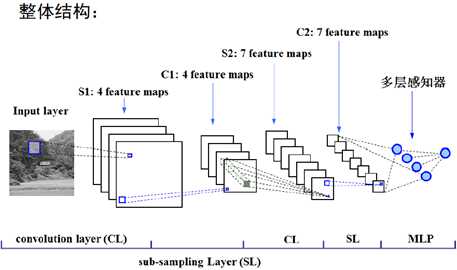
网络的训练:仍然采用误差反向传播算法。
2.AutoEncoder(自编码器)
目的:卷积神经网络的训练样本是带有标签的,但是很多问题是没有标签的,所以我们的自然想法就是能不能处理这一类问题。
解决的思路:在整个网络中让输出与输入相等,隐含层则可以理解为用于记录数据的特征。
核心思想
–将 input 输入一个 encoder 编码器,就会得到一个 code。这个 code 也就是输入的一个表示。
–通过增加一个 decoder 解码器,并采用信号重构的方式来评价这个 code 的质量。
–理想情况下,希望 decoder 所输出的信息(表达可能不一样,但本质上反应的是同一个模式)与输入信号input 是相同的。
–此时会产生误差,我们期望这个误差最小。
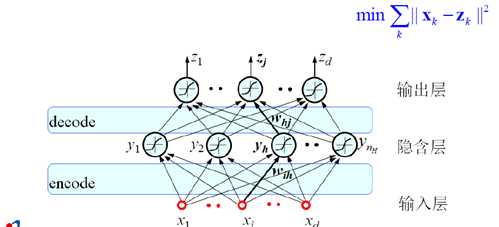
–将第一层输出的 code 当成第二层的输入信号,再次最小化重构误差,得到第二层的权重参数,同时获得第二层的code,即原始号的第二个表达。
–在训练当前层时,其它层固定不动。完成当前编码和解码任务。前一次"编码"和"解码"均不考虑。
–因此,这一过程实质上是一个静态的堆叠(stack)过程
–每次训练可以用BP算法对一个三层前向网络进行训练
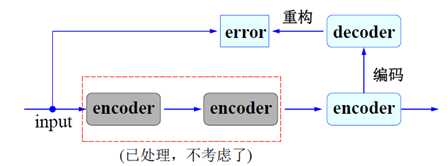
在完成 Autoencoder 的学习任务之后,在实际应用中,在解码阶段学习得到的权重将不进行考虑。因此,编码阶段获得的网络系统其实质是一种特征学习。层级越高,结构特征越大越明显。
对于分类任务,可以事先用 Autoencoder 对数据进行学习。然后以学习得到的权值作为始初权重,采用带有标签的数据对网络进行再次学习,即所谓的 fine-tuning。为了实现分类任务,需要在编码阶段的最后一层加上一个分类器,比如一个多层感知器(MLP)。
3.RNN
网络结构如下:(注意这里的标号都是向量和矩阵,代表了一个网络结构,如右侧的图示)
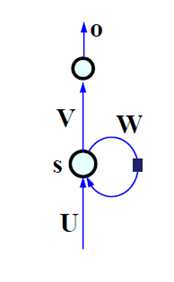

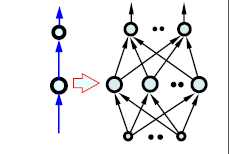
这里的W是产生记忆的源头,将输入按时间顺序展开得到下图(两个图是一样的,只是表示形式不同):
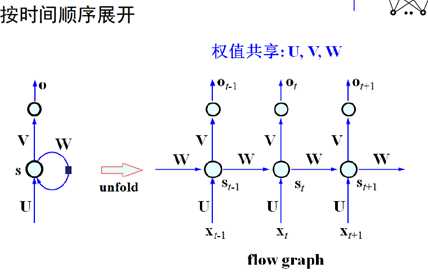
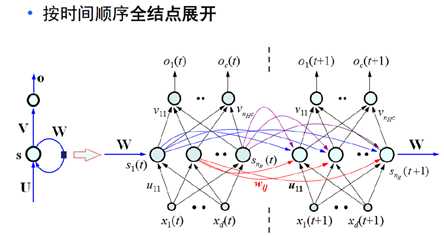
接下来就是如何训练如此庞大的一个网络,所以引进了一个方法LSTM
4.LSTM (Long Short Term Memory)
基本理念:一旦信息得到利用,我们希望该结点能释放(遗忘)这种累积效应,从而使网络更具有灵活性和自主学习性(依赖于学习内容来自我决定)。
它是在RNN网络结构的基础上改变了隐含层神经元的构成,具体如下:
由简单的输入、输出、隐含层自循环增加了三个门单元
-遗忘门:控制对细胞内部状 态的遗忘程度
-输入门:控制对细胞输入的 接收程度
-输出门:控制对细胞输出的 认可程度
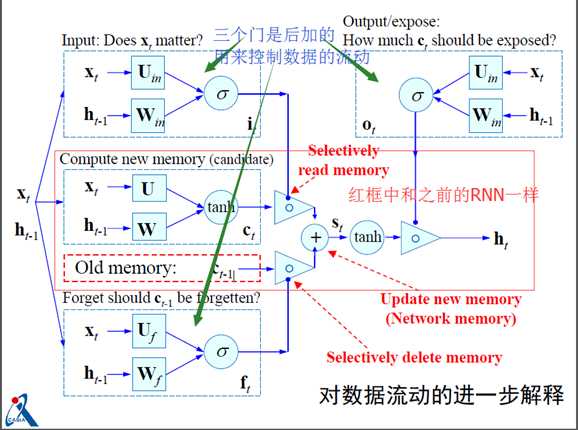
对应公式如下:
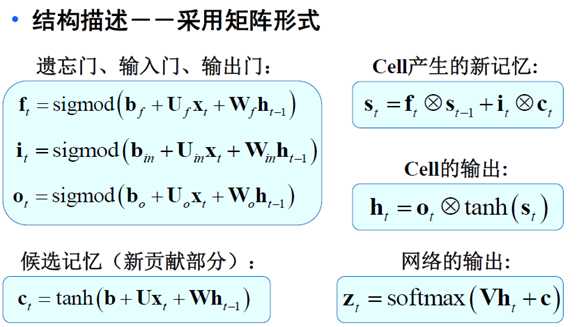
网络训练的目标是要估计如下矩阵:
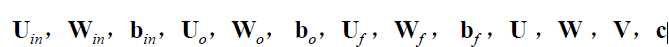
截图来源:http://pan.baidu.com/s/1sltG4bj
推荐文章:Yann LeCun、Yoshua Bengio和Geoffrey Hinton合作的一篇综述文章"Deep Learning":http://www.nature.com/nature/journal/v521/n7553/full/nature14539.html ,及其翻译:http://www.csdn.net/article/2015-06-01/2824811
标签:
原文地址:http://www.cnblogs.com/simayuhe/p/5399601.html