标签:
模式识别算法
肌电模式特征提取
普遍认为,肌电信号是一非稳态随机过程,它的幅值、方差、能量及频率因收缩等级的不同而不同,此外肌电信号信噪比低,所以可以把原始信号看作是超高维或者是无穷维的特征。特征的选择有几种类型:
1.对肌电信号过程进行物理建模,把其中一个或者多个物理量作为用于分类的特征,对于表面肌电信号进行建模分析,普遍采用Merlo提出的数学模型。基于大量动作电位的重叠及运动单位放电的非对称特性,表面肌电可以看出复杂的、非稳定随机信号。常用的肌电特征为 幅度、功率谱及小波系数(分别作用在信号的时域、频域及时频域)。如将肌电信号看成是零均值随机信号,那么它的幅度估计可以使用为标准差,并直接跟活动中动作单元的个数及放电率成比例。这里,信噪比代表了信号幅度特征中的随机成分,信噪比越大,肌电信号幅度特征表现越好。特征:
幅度
功率谱
小波系数
均方根和绝对均值:如果将肌电信号看成是高斯随机过程或者拉普拉斯随机过程(是什么?见文尾),均方根和绝对均值则分别是肌肉等力(是什么?)收缩(无疲劳)时信号幅值的极大似然估计。Clancy指出,正常肌电模型(等力、定姿态、无疲劳)位于高斯及拉普拉斯随机模型之间,且高斯模型稍优。 预处理收藏:对于多通道原始肌电信号,可以采用基于3-5阶AR模型的滤波器对信号进行白化处理(是什么?),以提高复制特征的置信度(是什么?)
频谱:常用于分析肌肉的疲劳特性以及动作单元募集的内部变化。影响肌电信号频谱的两个因素:一个是低频的动作电位发放率(<40Hz),一个是高频的动作电位在肌肉纤维内的传导形态(>40Hz)。肌电信号频谱是一种时变的信号,其直接跟肌肉的收缩强度、肌肉疲劳以及电极片间隔相关。即便是肌肉没有收缩状态变化,由于人体器官的内在特性,在等力收缩情况下,也应将肌电信号看成是非稳态信号。但是,有人指出肌肉位于不同等级收缩强度时(<80%MVC是什么?),500~1500ms内的肌肉信号可以近似看成是局部稳态的,所以频谱的一些特征也可用于肌电信号的实时处理。功率谱估计(PSD)是最常用的谱分析方法,其两个主要特征变量,中值频率和平均频率,能够提供肌电信号谱的基本信息。AR模型是计算PSD的方法之一,其阶数可以依靠AIC准则或者是最小描述长度(MDL)的方法。
小波变换:数学世界的“显微镜”,是信号时-频域分析的代表方法,解决傅里叶变换完全丢失了时域信息,对肌电信号瞬态分析无能为力的问题。小波变换能够反映信号局部特性,通过平移基本子波及变换比例尺就可以实现信号的多分辨率变换。
2.非建模方法,认为特征组合将要比单一特征获得更高的识别成功率。它包括特征选择(在原始特征向量维度中选择最优的子集)和特征投影(将原始特征向量分量进行线性或非线性组合得到新的特征集,如PCA)。
方法主要有:神经网络方法、模糊算法、概率算法、SVM
神经网络:具有拟合线性及非线性数据关系的能力,计算量较小,满足实时
模糊逻辑分类器:容易建立数据中难以察觉的模式,容易引入专家经验,鲁棒,可与神经网络结合
概率估计:高斯混合模型,隐马尔可夫模型
支持向量机:较强的小样本学习及泛化能力,不会陷入局部最小点
基于模式识别算法进行肌电模式识别有针对动作以及姿态两种不同的途径。以前多采用瞬态信号,但是每次控制指令的发起需要进行一次肌肉收缩的动作,控制缺乏实时性。
Engleart详细比较了使用肌电信号暂态和稳态的分类情况,指出使用稳态肌电信号也可以获得很高成功率(难度肯定有),因为其是实时检测肌电信号各种可能模式,很适合用于实时感官控制。他使用了“叠加输出”的算法
在线学习指的是在已有模式分类器基础上,持续性地对新模式样本进行学习的过程。
目标:肌电信号分析处理需要调节自身参数以最小化识别错误率,即学习肌电时变模式以实时适应信号源的变更。
挑战:由于肌肤阻抗、电极位置、肌肉疲劳、出汗等不同情况,不同个体不同时期的肌电信号的模式不尽相同。
需要解决的二个基本问题:一是如何学习,即如何根据当前情况确定再学习的必要性;二是怎样学习,即如何确定再学习所采用样本以及具体的学习算法。
模式识别领域的难点:有效的在线非监督式学习
补充
拉普拉斯过程:
如果随机变量的的概率密度函数分布为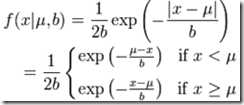
那么它就是拉普拉斯分布,记为x-Laplace(u,b),其中,μ 是位置参数,b>0 是尺度参数。如果 μ = 0,那么,正半部分恰好是尺度为 1/b(或者b,看具体指数分布的尺度参数形式) 的指数分布的一半。拉普拉斯分布的概率密度函数让我们联想到正态分布,但是,正态分布是用相对于 μ 平均值的差的平方来表示,而拉普拉斯概率密度用相对于平均值的差的绝对值来表示。因此,拉普拉斯分布的尾部比正态分布更加平坦。
肌肉在收缩时其长度不变而只有张力增加,这种收缩称为等长收缩,又称为静力收缩。
肌肉等长收缩时由于长度不变,因而不能克服阻力做机械功。等长收缩可以使某些关节保持一定的位置,为其他关节的运动创造条件。
白化
使用PCA降低数据维度。在一些算法中还需要一个与之相关的预处理步骤,这个预处理过程称为白化(一些文献中也叫sphering)。举例来说,假设训练数据是图像,由于图像中相邻像素之间具有很强的相关性,所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性;更正式的说,我们希望通过白化过程使得学习算法的输入具有如下性质:(i)特征之间相关性较低;(ii)所有特征具有相同的方差。
标签:
原文地址:http://www.cnblogs.com/yuanhao11/p/5406035.html