标签:
| Time Limit: 2000MS | Memory Limit: 10000K | |
| Total Submissions: 7584 | Accepted: 3518 |
Description
Input
Output
Sample Input
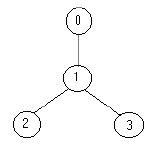
4 0:(1) 1 1:(2) 2 3 2:(0) 3:(0) 5 3:(3) 1 4 2 1:(1) 0 2:(0) 0:(0) 4:(0)
Sample Output
1 2
Source
题意:一个游戏有n个点,在某些点上放置哨兵,每个哨兵可以监控和它有边相连的点,问监视所有的点需要的最少的哨兵数.
分析:树形DP,dp[i][0]表示第i个点不放哨兵需要的以i为根节点的子树最少需要的哨兵,dp[i][1]代表第i个点放哨兵需要的以i为根节点的子树最少需要的哨兵
如果某一点不放哨兵,那么他的子节点都需要设一个哨兵。
如果某一点放哨兵,那么就从子节点放还是不放中选最小的.
#include <iostream> #include <stdio.h> #include <string.h> #include <algorithm> #define N 1505 using namespace std; int head[N]; struct Edge{ int u,v,next; }edge[N]; void addEdge(int u,int v,int &k){ edge[k].u = u,edge[k].v = v; edge[k].next = head[u];head[u] = k++; } int dp[N][2]; int indegree[N]; void dfs(int u){ for(int k = head[u];k!=-1;k=edge[k].next){ int v = edge[k].v; dfs(v); dp[u][0]+=dp[v][1]; ///父亲不放,孩子必放 dp[u][1]+=min(dp[v][0],dp[v][1]); ///父亲放了,孩子在放与不放之间选哨兵数小的 } } int main() { int n; while(scanf("%d",&n)!=EOF) { memset(indegree,0,sizeof(indegree)); memset(head,-1,sizeof(head)); int u,v,t; int tot=0; for(int i=0;i<n;i++){ dp[i][0] = 0; dp[i][1] = 1; scanf("%d:(%d)",&u,&t); for(int j=0;j<t;j++){ scanf("%d",&v); addEdge(u,v,tot); indegree[v]++; //printf("%d %d\n",u,v); } } int root; for(int i=0;i<n;i++) if(indegree[i]==0) {root=i;break;} //printf("%d\n",root); dfs(root); printf("%d\n",min(dp[root][0],dp[root][1])); } return 0; }
标签:
原文地址:http://www.cnblogs.com/liyinggang/p/5410667.html