标签:
部门在各个团队推广软件通用技能矩阵工具,希望通过度量找到能力薄弱点,引导团队进行改进。从我们团队的数据上看,团队在数据结构和算法上的短板明显,需要加强,这也是写这篇文章的背后的初衷。
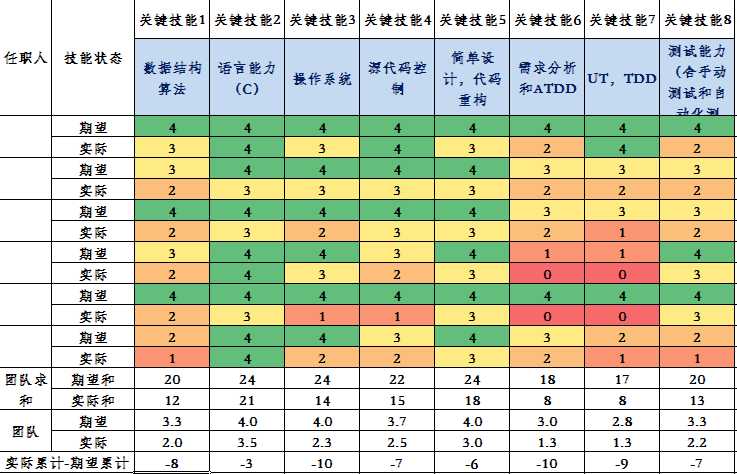
数据结构和算法是程序员的基本技能,也是大牛程序员的试金石。Linus大神就曾说过:"bad programer care about code, good progamer care about data"。平时工作中,可能大家觉得用不到复杂的数据结构,数组、顶多链表就够用了,但是实际情况可能是因为不了解其他的数据结构以及各自的适用场景,只有数组或者链表可供选择而已。
作为负责Linux Kernel和Driver开发的团队,Linux Kernel中运用了大量的数据结构类型,这其中,以RB-tree(Red Block Tree,红黑树)的使用最为频繁,比如内存管理、文件系统、网络子系统等核心子系统都大量使用了RB-tree。RB-tree算法复杂,很值得研究学习,可惜的是,在我所能看到的书和文章中,还没看到真正能讲清楚的,这也是挑选RB-tree作为这次分享主题的主要动机。
我研究问题有个习惯,喜欢探索什么样的的需求导致它的出现,然后经过哪些历史演变最终变成现在的样子。揣摩它背后的思路过程,比只看那繁杂的具体实现、一堆的规则定义要有趣的多,有意义的多。比如《数据结构和算法分析》(Mark Allen Weiss著)书中给的红黑树的4条规则:
那么问题来了:为什么满足这4条规则就是RB-tree,什么的需求推导出这些规则的,这些规则都能带来什么价值?
在RB-tree(1972年)出现之前,已经有了AVL tree(1962年)和2-3-4 tree,2-3-4 tree的出现是为了获得比AVL tree的更快、更稳定的插入删除时间(最差情况),但是2-3-4 tree本身也有个问题:需要处理的场景多,节点模型不统一,实现复杂。RB-tree的出现就是为了解决2-3-4 tree的这些问题。本文不分析AVL tree和2-3-4 tree,如有需要请自行查阅wikipedia,具体比较如下。
| 列1 | AVL Tree | 2-3-4 Trees | Red Black Trees |
| Goods | • Balanced • O(log N) search time |
• Balanced • O(log N) search time • faster real-time bounded insertion and deletion |
• Balanced • O(log N) search time • faster real-time bounded insertion and deletion • same node structures |
| Bads | • slower real-time bounded insertion and deletion | • Different node structures • large number of special cases involved in operations on the tree |
• slightly slower search time |
如下图所示,RB-tree等价于2-3-4 tree,是2-3-4 tree实现的一种优化方案。
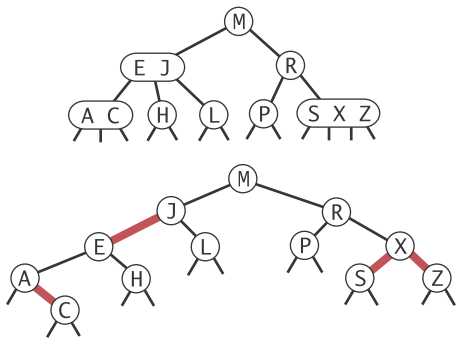
RB-tree的着色是为了构建2-3-4 tree中的3-node、4-node节点模型,RB-tree中一条红线相连的2个节点,等价于2-3-4 tree中的3-node节点;RB-tree中两条连续的红线相连的3个节点,等价于2-3-4 tree中的4-node节点。这就是RB-tree规则(1)的由来。
RB-tree规则(4)是2-3-4 tree的特征,那么自然也适用于RB-tree。
红色作为RB-tree 3-node、4-node节点的内部连接器,红色节点有个隐含含义:它还有父节点。所以根节点不需要着红色,这就是RB-tree规则(2)的由来。如果在变换过程中,根节点着成了红色,直接改成黑色即可。
可见,规则(1)、(2)、(4)都是RB-tree对2-3-4 tree的一种自然解释。目前为止,我们唯独没有分析的规则(3),是RB-tree区别于2-3-4 tree的重要规则,也是最核心的规则。这也是下一节分析的重点。
在规则(1)、(2)、(4)下,如方案A,RB-tree对3-node有2种表达形式,对4-node有5种表达形式,加上2-node的1种表达形式,总共存在8个基本结构,这就代表在对RB-tree插入、删除操作时需要考虑8种场景,这么多的场景需要处理,势必会带来实现的复杂和效率的降低,这正是2-3-4 tree最大的问题,也是RB-tree首要解决的问题。
方案B的思路是通过把4-node的5种表达形式统一规约到4.5这个结构上,把4-node的基本结构减少到一个,减少处理场景,来精简实现提升效率。这正是规则(3)的目的,把4.1到4.4这4个结构排除在外,只留下4.5这一种结构。方案B中展示了结构4.1、4.2、4.3、4.4是如何通过旋转来转变为结构4.5。
方案C在方案B的基础上更近一步,将结构3.2通过左旋转变为结构3.1,将3-node结构规约为一种结构,这个方案又叫LLRB(left-leaning RB-tree),它的基本结构与2-3-4 tree一一对应,实现简单,而且算法统一。
下图演示了RB-tree的插入过程。RB-tree插入新节点时,保证插入到叶节点处,而且着色为红色。插入和删除操作可能会破坏规则(3),这就需要对数结构进行再平衡操作,2-3-4 tree的再平衡手段是节点分裂和合并,在RB tree中则是着色翻转(color flip)和旋转(rotation)。
着色翻转保证当出现5-node的情况时,把其分解成2个3-node,并将中间节点上送给父节点。
节点旋转分为左旋和右旋。节点P左旋即把P作为P的右子节点的左子节点,节点P右旋即把P作为P的左子节点的右子节点。
下图中分别按2-node,3-node,4-node情况,展示了插入新节点后的旋转和着色翻转步骤。方案B多一组(b)处理步骤,共1+2=3次旋转操作;方案C多一组(c)处理步骤,也是3次旋转操作。可见从实现效率上来看,方案B和方案C是相同的,但是方案C的基本结构少,算法统一,实现简单,更易于理解。
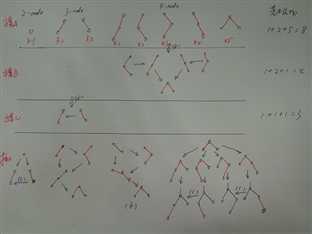
对照Linux Kernel中的RB-tree中的插入函数实现,可以发现和上图中的方案B插入实现是完全一致的。
void rb_insert_color(struct rb_node *node, struct rb_root *root)
{
struct rb_node *parent, *gparent;
while ((parent = rb_parent(node)) && rb_is_red(parent))
{
gparent = rb_parent(parent);
if (parent == gparent->rb_left)
{
{
register struct rb_node *uncle = gparent->rb_right;
if (uncle && rb_is_red(uncle))
{
rb_set_black(uncle);
rb_set_black(parent);
rb_set_red(gparent);
node = gparent;
continue;
}
}
if (parent->rb_right == node)
{
register struct rb_node *tmp;
__rb_rotate_left(parent, root);
tmp = parent;
parent = node;
node = tmp;
}
rb_set_black(parent);
rb_set_red(gparent);
__rb_rotate_right(gparent, root);
} else {
{
register struct rb_node *uncle = gparent->rb_left;
if (uncle && rb_is_red(uncle))
{
rb_set_black(uncle);
rb_set_black(parent);
rb_set_red(gparent);
node = gparent;
continue;
}
}
if (parent->rb_left == node)
{
register struct rb_node *tmp;
__rb_rotate_right(parent, root);
tmp = parent;
parent = node;
node = tmp;
}
rb_set_black(parent);
rb_set_red(gparent);
__rb_rotate_left(gparent, root);
}
}
rb_set_black(root->rb_node);
}
--EOF--
标签:
原文地址:http://www.cnblogs.com/wahaha02/p/5409865.html