标签：
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 5365 | Accepted: 3585 |
Description
Input
Output
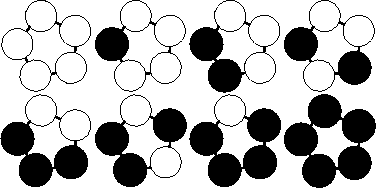For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.Sample Input
1 1 2 1 2 2 5 1 2 5 2 6 6 2 0 0
Sample Output
1 2 3 5 8 13 21
/*
poj 2409 Polya模板题
旋转：
L = sum(k^Ci)/n(i = 0,1.....n-1) 求出每次旋转i位的和
顺时针旋转i格的置换中,循环的个数为GCD(n,i),长度为n/GCD(n,i).
so Ci = GCD(n,i)
翻转：
当n为偶数时,n/2个的置换Ci = n/2； n/2个的置换Ci = n/2-1
当n为奇数时,n个置换Ci = n/2+1
hhh-2016-04-19 10:06:23
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <map>
#include <algorithm>
#include <functional>
#include <math.h>
using namespace std;
#define lson (i<<1)
#define rson ((i<<1)|1)
typedef long long ll;
const int maxn = 100040;
ll gcd(ll a, ll b) {
return b ? gcd(b, a%b) : a;
}
ll pow(ll a, ll b)
{
ll res = 1;
while(b)
{
if(b&1) res *= a;
a = a*a;
b >>= 1;
}
return res;
}
ll polya(ll n,ll k)
{
ll ans = 0;
for(int i = 1; i <= n; i++)
{
ans += pow(k,gcd(n,i));
}
if(n & 1)
ans += pow(k,n/2+1)*n;
else
{
ans += pow(k,n/2)*(n/2);
ans += pow(k,n/2+1)*(n/2);
}
return ans/(n*2);
}
int main()
{
ll n,c;
while(scanf("%I64d%I64d",&c,&n) != EOF)
{
if(!n && !c)
break;
printf("%I64d\n",polya(n,c));
}
return 0;
}
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 7525 | Accepted: 3132 |
Description
Input
Output
Sample Input
4 5 -1
Sample Output
21 39
/*
poj 1286 polya(euler优化)
依旧是模板题，只是在上面加了优化
优化：(黑书)
以前都是直接枚举i来求解。 但是可以考虑通过枚举循环节的长度L,然后计算有多少个i
L = n/(GCD(n,i)) -> GCD(n,i) = n/L
不妨设 a = n/L = GCD(n,i) , 不妨设 i = a*t -> GCD(n,i) = GCD(a*L,a*t) = a
所以只有 GCD(L,t) = 1是才行。 0 ≤ i <n ---> 0 ≤ t < L(n/a)
即小于L且与L互质的个数,这个用欧拉函数解决
hhh-2016-04-19 11:14:49
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <map>
#include <algorithm>
#include <functional>
#include <math.h>
using namespace std;
#define lson (i<<1)
#define rson ((i<<1)|1)
typedef long long ll;
const int maxn = 100040;
ll euler(ll n)
{
ll ans = n;
for(int i = 2;i*i <= n;i++)
{
if(n % i == 0)
{
ans -= ans/i;
while(n % i == 0)
{
n /= i;
}
}
}
if(n > 1) ans -= ans/n;
return ans;
}
ll gcd(ll a, ll b) {
return b ? gcd(b, a%b) : a;
}
ll Pow(ll a, ll b)
{
ll res = 1;
while(b)
{
if(b&1) res *= a;
a = a*a;
b >>= 1;
}
return res;
}
ll polya(ll n,ll k)
{
ll ans = 0;
for(ll i = 1; i <= n; i++)
{
if(n % i == 0) //枚举循环节的长度
ans += Pow(k,i)*euler(n/i);
}
if(n & 1)
ans += Pow(k,n/2+1)*n;
else
{
ans += Pow(k,n/2)*(n/2);
ans += Pow(k,n/2+1)*(n/2);
}
return ans/(n*2);
}
int main()
{
ll n;
while(scanf("%I64d",&n) != EOF)
{
if(n == -1)
break;
if(n == 0)
printf("0\n");
else
printf("%I64d\n",polya(n,3));
}
return 0;
}
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 122768/62768 K (Java/Others)
Total Submission(s): 1426 Accepted Submission(s): 610
/*
HDU 3923 Ploya定理+逆元
裸Polya计数,只是在后面求个逆元即可
hhh-2016-04-19 11:40:12
*/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <vector>
#include <map>
#include <algorithm>
#include <functional>
#include <math.h>
using namespace std;
#define lson (i<<1)
#define rson ((i<<1)|1)
typedef long long ll;
const int maxn = 100040;
const int mod = 1000000007;
ll euler(ll n)
{
ll ans = n;
for(int i = 2;i*i <= n;i++)
{
if(n % i == 0)
{
ans -= ans/i;
while(n % i == 0)
{
n /= i;
}
}
}
if(n > 1) ans -= ans/n;
return ans%mod;
}
ll Pow(ll a, ll b)
{
ll res = 1;
a %= mod;
while(b)
{
if(b&1) res =res*a%mod;
a = a*a%mod;
b >>= 1;
}
return res%mod;
}
ll polya(ll n,ll k)
{
ll ans = 0;
for(ll i = 1; i <= n; i++)
{
if(n % i == 0) //枚举循环节的长度
ans =(ans+Pow(k,i)*euler(n/i)%mod)%mod;
}
if(n & 1)
ans =(ans+Pow(k,n/2+1)*n%mod)%mod;
else
{
ans = (ans+Pow(k,n/2)*(n/2)%mod)%mod;
ans = (ans+Pow(k,n/2+1)*(n/2)%mod)%mod;
}
ll t = Pow(n*2,mod-2); //求逆元
return ans*t%mod;
}
int main()
{
ll n,c;
int T,cas = 1;
scanf("%d",&T);
while(T--)
{
scanf("%I64d%I64d",&c,&n);
printf("Case #%d: ",cas++);
printf("%I64d\n",polya(n,c));
}
return 0;
}
Time Limit: 2000/2000 MS (Java/Others) Memory Limit: 65535/32768 K (Java/Others)
Total Submission(s): 637 Accepted Submission(s): 313
//hdu 3547 用C种颜色对正方形的八个顶点染色
//如果用1234表示顶面 5678表示底面 //1.绕着相互对立的两个面旋转，有90度，180度，270度，所以总共有3*3=9种情况。 // 绕90 or 270. {1 2 3 4} {5,6,7,8} 2个循环节 总共有6中情况 // 绕180 {1,3}{2,4}{5,7}{6,8} 4个循环节 共有3种情况 //2.绕着相互对立的两个边旋转，有180度这样，所以总共有6*1=6种。 // {1,7}{2,8}{3,4}{5,6} 4个循环节 //3.绕着对角点旋转，有120度，240度这样，所以总共有4*2=8种。 // {2,5,7}{1,3,8}{6}{4} 4个循环节 //4.不动，有一种。 {1}{2}{3}{4}{5}{6}{7}{8} 8个循环节 //假设有C中颜色 则共有C^8 + 17*C^4 + 6*C^2 import java.math.BigInteger; import java.util.Scanner; public class Main { public static void main(String[] args) { // TODO 自动生成的方法存根 Scanner cin = new Scanner(System.in); int T = cin.nextInt(); int cas = 1; while(T>0){ BigInteger c = cin.nextBigInteger(); BigInteger t1 = c.pow(8); BigInteger t2 = c.pow(4); BigInteger t3 = c.pow(2); // System.out.println("t1:"+t1); // System.out.println("t2:"+t2); // System.out.println("t3:"+t3); t2 = t2.multiply(BigInteger.valueOf(17)); t3 = t3.multiply(BigInteger.valueOf(6)); BigInteger ans = t1.add(t2).add(t3); String tans = ans.divide(BigInteger.valueOf(24)).toString(); int len = tans.length(); System.out.print("Case " + cas+": "); if(len <= 15) System.out.println(tans); else System.out.println(tans.substring(len-15)); cas++; T--; } } }
标签：
原文地址：http://www.cnblogs.com/Przz/p/5415678.html
