标签:
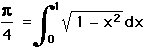
and without using the binomial theorem or integration (not invented yet) painstakingly came up with a formula for  to be
to be
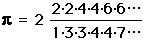 .
.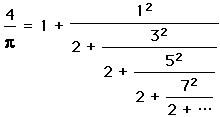 .
.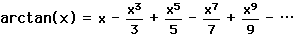 ,
,and the fact that arctan(1) =  /4 to obtain the series
/4 to obtain the series
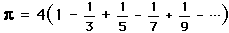 .
.Unfortunately, this series converges to slowly to be useful, as it takes over 300 terms to obtain a 2 decimal place precision. To obtain 100 decimal places of  , one would need to use at least 10^50 terms of this expansion!
, one would need to use at least 10^50 terms of this expansion!
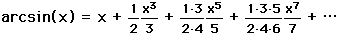 ,
,and the fact that arctan(1/2) =  /6 to obtain the series
/6 to obtain the series
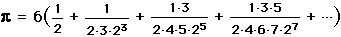 .
.This arcsine series converges much faster than using the arctangent. (Actually, Newton used a slightly different expansion in his original text.) This expansion only needed 22 terms to obtain 16 decimal places for  .
.
 ,
,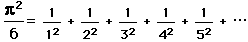
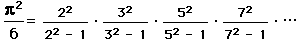
 in terms of the Fibonacci numbers,
in terms of the Fibonacci numbers,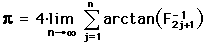 .
.标签:
原文地址:http://blog.csdn.net/u013077144/article/details/51212058