标签:
本文主要介绍三类参数估计方法-最大似然估计MLE、最大后验概率估计MAP及贝叶斯估计。
1、最大似然估计MLE
首先回顾一下贝叶斯公式
这个公式也称为逆概率公式,可以将后验概率转化为基于似然函数和先验概率的计算表达式,即
最大似然估计就是要用似然函数取到最大值时的参数值作为估计值,似然函数可以写做
由于有连乘运算,通常对似然函数取对数计算简便,即对数似然函数。最大似然估计问题可以写成
这是一个关于的函数,求解这个优化问题通常对
求导,得到导数为0的极值点。该函数取得最大值是对应的
的取值就是我们估计的模型参数。
以扔硬币的伯努利实验为例子,N次实验的结果服从二项分布,参数为P,即每次实验事件发生的概率,不妨设为是得到正面的概率。为了估计P,采用最大似然估计,似然函数可以写作
得到参数p的最大似然估计值为
可以看出二项分布中每次事件发的概率p就等于做N次独立重复随机试验中事件发生的概率。
如果我们做20次实验,出现正面12次,反面8次
那么根据最大似然估计得到参数值p为12/20 = 0.6。
2、最大后验估计MAP
最大后验估计与最大似然估计相似,不同点在于估计的函数中允许加入一个先验
,也就是说此时不是要求似然函数最大,而是要求由贝叶斯公式计算出的整个后验概率最大,即
注意这里P(X)与参数无关,因此等价于要使分子最大。与最大似然估计相比,现在需要多加上一个先验分布概率的对数。在实际应用中,这个先验可以用来描述人们已经知道或者接受的普遍规律。例如在扔硬币的试验中,每次抛出正面发生的概率应该服从一个概率分布,这个概率在0.5处取得最大值,这个分布就是先验分布。先验分布的参数我们称为超参数(hyperparameter)即
同样的道理,当上述后验概率取得最大值时,我们就得到根据MAP估计出的参数值。给定观测到的样本数据,一个新的值发生的概率是
下面我们仍然以扔硬币的例子来说明,我们期望先验概率分布在0.5处取得最大值,我们可以选用Beta分布即
其中Beta函数展开是
当x为正整数时
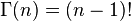
Beta分布的随机变量范围是[0,1],所以可以生成normalised probability values。下图给出了不同参数情况下的Beta分布的概率密度函数
我们取,这样先验分布在0.5处取得最大值,现在我们来求解MAP估计函数的极值点,同样对p求导数我们有
得到参数p的的最大后验估计值为
和最大似然估计的结果对比可以发现结果中多了这样的pseudo-counts,这就是先验在起作用。并且超参数越大,为了改变先验分布传递的belief所需要的观察值就越多,此时对应的Beta函数越聚集,紧缩在其最大值两侧。
如果我们做20次实验,出现正面12次,反面8次,那么
那么根据MAP估计出来的参数p为16/28 = 0.571,小于最大似然估计得到的值0.6,这也显示了“硬币一般是两面均匀的”这一先验对参数估计的影响。
3 贝叶斯估计
贝叶斯估计是在MAP上做进一步拓展,此时不直接估计参数的值,而是允许参数服从一定概率分布。回顾一下贝叶斯公式
现在不是要求后验概率最大,这样就需要求,即观察到的evidence的概率,由全概率公式展开可得
当新的数据被观察到时,后验概率可以自动随之调整。但是通常这个全概率的求法是贝叶斯估计比较有技巧性的地方。
那么如何用贝叶斯估计来做预测呢?如果我们想求一个新值的概率,可以由
来计算。注意此时第二项因子在上的积分不再等于1,这就是和MLE及MAP很大的不同点。
我们仍然以扔硬币的伯努利实验为例来说明。和MAP中一样,我们假设先验分布为Beta分布,但是构造贝叶斯估计时,不是要求用后验最大时的参数来近似作为参数值,而是求满足Beta分布的参数p的期望,有
注意这里用到了公式
当T为二维的情形可以对Beta分布来应用;T为多维的情形可以对狄利克雷分布应用
根据结果可以知道,根据贝叶斯估计,参数p服从一个新的Beta分布。回忆一下,我们为p选取的先验分布是Beta分布,然后以p为参数的二项分布用贝叶斯估计得到的后验概率仍然服从Beta分布,由此我们说二项分布和Beta分布是共轭分布。在概率语言模型中,通常选取共轭分布作为先验,可以带来计算上的方便性。最典型的就是LDA中每个文档中词的Topic分布服从Multinomial分布,其先验选取共轭分布即Dirichlet分布;每个Topic下词的分布服从Multinomial分布,其先验也同样选取共轭分布即Dirichlet分布。
根据Beta分布的期望和方差计算公式,我们有
可以看出此时估计的p的期望和MLE ,MAP中得到的估计值都不同,此时如果仍然是做20次实验,12次正面,8次反面,那么我们根据贝叶斯估计得到的p满足参数为12+5和8+5的Beta分布,其均值和方差分别是17/30=0.567, 17*13/(31*30^2)=0.0079。可以看到此时求出的p的期望比MLE和MAP得到的估计值都小,更加接近0.5。
综上所述我们可以可视化MLE,MAP和贝叶斯估计对参数的估计结果如下
个人理解是,从MLE到MAP再到贝叶斯估计,对参数的表示越来越精确,得到的参数估计结果也越来越接近0.5这个先验概率,越来越能够反映基于样本的真实参数情况。
原文地址:http://blog.csdn.net/yangliuy/article/details/8296481
参考文献
Gregor Heinrich, Parameter estimation for test analysis, technical report
Wikipedia Beta分布词条 , http://en.wikipedia.org/wiki/Beta_distribution
标签:
原文地址:http://blog.csdn.net/wtq1993/article/details/51213204