标签:
Description




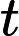

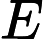

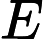

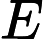





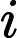

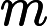

Input







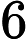



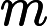
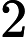





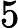





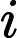

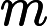

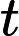




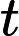




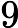









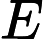

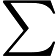
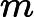



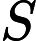





Output
Sample Input
2 5 4 1 3 1 2 3 2 2 3 4 10 2 1 5 3 3 3 4 5 3 1 1 2 1 2
Sample Output
Case #1: 3 3 4 Case #2: Evil John
Hint
In the first case, it will take Bessie 1 minute travelling to the 3rd block, and it will take Elsie 3 minutes travelling to the 3rd block. It will take Bessie 3 minutes travelling to the 4th block, and it will take Elsie 3 minutes travelling to the 4th block. In the second case, it is impossible for them to meet.
题意
有 N个点 n<=100000 ,m《=10000个集合,在同一个集合中的人意两个点的距离都相等,不同的集合时间不一定相同, 一个人从1 出发,一个人从n出发求 二人相遇的最时间
思路:
如果按普通的写法 则需要建立很多的边,边太多是存不下的,所以要缩图,缩图的方法
这样就可以了 ,保证了集合内的点人意点都是time 哈
但是 使用普通的SPFA 就会超时!!QAQ
需要是用 dijktra + 优先队列
套了个最短路优化模版 就可以了
#include <queue>
#include <vector>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#define pb push_back
#define mp make_pair
#define sz(x) ((int)(x).size())
using namespace std;
const int N = 1000100*2;
const long long INF = 1e18;
int n, m;
long long dis[N];
long long dis1[N];
long long dis2[N];
long long f[N];
bool vis[N];
struct Node
{
long long d;
int e;
bool operator < (const Node x) const
{
return x.d < d;
}
Node(long long d, int e):d(d), e(e) {}
};
vector<pair<int,long long > > V[N];
void dijkstra(int s)
{
priority_queue<Node> q;
fill(dis + 1, dis + n+2*m + 1, INF);
fill(vis + 1, vis + n+2*m + 1, false);
q.push(Node(0, s));
dis[s] = 0;
while(!q.empty())
{
Node deq = q.top();
q.pop();
if(vis[deq.e])
continue;
vis[deq.e] = true;
for(int i = 0; i < sz(V[deq.e]); i++)
{
int e = V[deq.e][i].first;
long long w = V[deq.e][i].second;
if(dis[deq.e] < dis[e] - w)
{
dis[e] = dis[deq.e] + w;
q.push(Node(dis[e], e));
}
}
}
}
void add_edge(int a,int b,long long c)
{
V[a].push_back(make_pair(b, c));
}
long long max(long long a,long long b)
{
if(a>b)
return a;
return b;
}
long long min(long long a,long long b)
{
if(a>b)return b;
return a;
}
int main()
{
int T;
scanf("%d",&T);
int CASE=1 ;
while(T--)
{
scanf("%d%d",&n,&m);
int fc = n+1;
for(int i = 1; i<=n+m*2+1; i++)
V[i].clear();
long long time ;
int y;
for(int i = 1; i<=m; i++)
{
scanf("%lld%d",&time,&y);
int temp ;
for(int j = 1; j<=y; j++)
{
scanf("%d",&temp);
add_edge(temp,fc,0);
add_edge(fc+1,temp,0);
}
add_edge(fc,fc+1,time);
fc+=2;
}
dijkstra(1);
memcpy(dis1,dis,sizeof(dis));
dijkstra(n);
memcpy(dis2,dis,sizeof(dis));
long long minv = INF;
for(int i =1 ; i<=n; i++)
{
f[i] = max(dis1[i],dis2[i]);
minv = min(minv,f[i]);
}
printf("Case #%d: ",CASE++);
if(minv>=INF)
{
printf("Evil John\n");
}
else
{
printf("%lld\n",minv);
int flagc = 0;
for(int i = 1; i<=n; i++)
{
if(f[i]==minv)
{
if(!flagc)
{
printf("%d",i);
flagc = 1;
}
else
printf(" %d",i);
}
}
printf("\n");
}
}
return 0;
}
标签:
原文地址:http://blog.csdn.net/theflowerofac/article/details/51213158