标签:
树
树是一种非线性的数据结构,是n(n>=0)个结点的有限集。
(1)在任意一棵树中,有且仅有一个特定的根节点。如图点A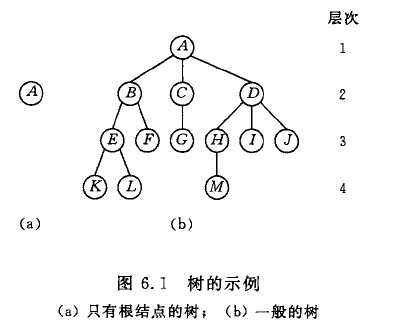
(2)节点拥有的子树数称为结点的度。图中A的度为3,C的度为1
(3)度为0的结点称为叶子或终端结点。如图KLM点
(4)度不为0的结点称为非终端结点或者分支结点。如图A B C...
(5)数的度是树内各结点的度的最大值,如图树的度是3
(6)节点的子树的根称为该结点的孩子,左侧的为左孩子,右侧的为右孩子。
相应的,该结点称为孩子的双亲
(7)树中结点的最大层次称为树的深度或高度。图所示的树的深度为4
(8)将树中结点的各子树看成从左到右是有次序(即左孩子不能和右孩子互换)
则称该树为有序树,否则为无序树。
(9)森林是m(m>=0)棵互不相交的树的集合
二叉树
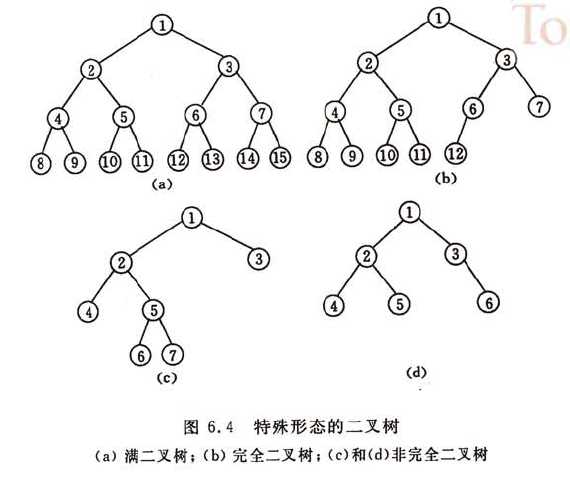
二叉树是一种特殊的树形结构,它的每个结点至多只有两颗子树,即二叉树中不存在度大于2的结点,
并且,二叉树的子树有左右之分,其次序不能任意颠倒。
(1)一棵深度为k且有2k - 1 个结点的二叉树称为 满二叉树,如图a
(2)深度为k的,有n个结点的二叉树,当且仅当其每一个结点都与深度为k的
满二叉树中编号从1至n的结点一一对应时,称为 完全二叉树。如图b
(3)二叉树的第i层上至多只有2i-1 个结点(i>=1)
(4)深度为k的二叉树至多有2k - 1个结点(k>=1)
二叉树的存储结构
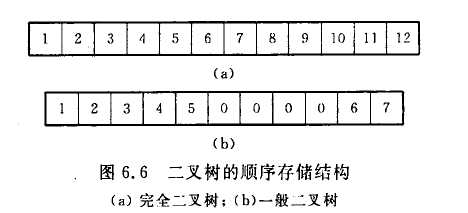
1.顺序存储结构
用一组地址连续的存储单元一次自上而下,自左而右存储完全二叉树的结点元素,注意这种存储结构仅适用于完全二叉树,“0”表示不存在此结点
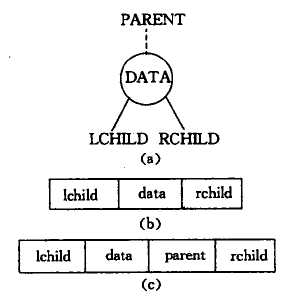
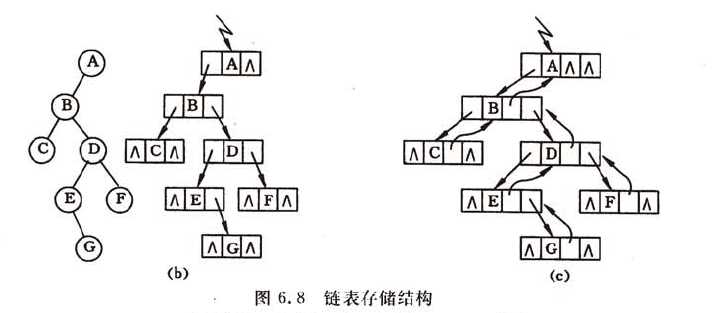
2.链式存储结构
非连续的存储结构,利用指针域把各节点连接构成链式,分别有二叉链表(数据域和指向左右子树的指针构成,下图b)和三叉链表法(数据域、指向双亲结点的指针和指向左右子树的指针构成,下图c)。
二叉树的遍历
先序遍历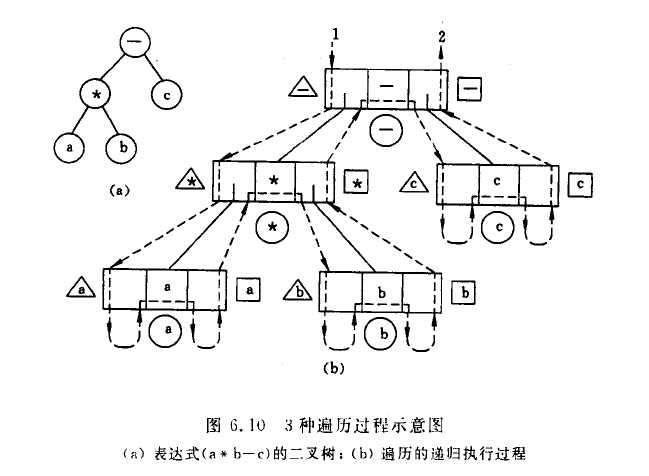
若二叉树为空,则空操作,否则
(1)访问根节点
(2)先序遍历左子树 先序遍历:- * a b c
(3)先序遍历右子树
中序遍历
若二叉树为空,则空操作,否则
(1)中序遍历左子树
(2)访问根节点 中序遍历:a * b - c
(3)中序遍历右子树
后序遍历
若二叉树为空,则空操作,否则
(1)后序遍历左子树
(2)后序遍历右子树 后序遍历:a b * c -
(3)访问根节点
二叉树的实现:
1 #include<stdio.h> 2 #include<stdlib.h> 3 typedef char ElemType; //数据类型 4 typedef int Status; //返回值类型 5 #define ERROR 0 6 #define OK 1 7 //定义二叉树结构 8 typedef struct BiTNode{ 9 ElemType data; //数据 10 struct BiTNode *lChild, *rChlid; //左右子树指针 11 }BiTNode, *BiTree; 12 13 //创建二叉树 14 Status CreateBiTree(BiTree *T) 15 { 16 ElemType ch; 17 ElemType c; 18 scanf("%c", &ch); 19 c = getchar(); 20 if (‘ ‘ == ch) 21 *T = NULL; 22 else 23 { 24 *T = (BiTree)malloc(sizeof(BiTNode)); 25 if (!(*T)) 26 exit(ERROR); 27 (*T)->data = ch; 28 printf("输入%c的左孩子结点,空格表示无此结点:", ch); 29 CreateBiTree(&(*T)->lChild); 30 printf("输入%c的右孩子结点,空格表示无此结点:", ch); 31 CreateBiTree(&(*T)->rChlid); 32 } 33 34 return OK; 35 } 36 37 //先序遍历二叉树 38 Status TraverseBiTree(BiTree T) 39 { 40 if (!T) return ERROR; 41 printf("%c ", T->data); 42 TraverseBiTree(T->lChild); 43 TraverseBiTree(T->rChlid); 44 return OK; 45 } 46 47 //中序遍历二叉树 48 Status InOrderBiTree(BiTree T) 49 { 50 if (!T) return ERROR; 51 InOrderBiTree(T->lChild); 52 printf("%c ", T->data); 53 InOrderBiTree(T->rChlid); 54 return OK; 55 } 56 57 //后序遍历二叉树 58 Status PostOrderBiTree(BiTree T) 59 { 60 if (NULL == T) return ERROR; 61 PostOrderBiTree(T->lChild); 62 PostOrderBiTree(T->rChlid); 63 printf("%c ", T->data); 64 return OK; 65 } 66 67 68 //二叉树的深度 69 int TreeDeep(BiTree T) 70 { 71 int deep = 0; 72 if (T) 73 { 74 int leftdeep = TreeDeep(T->lChild); 75 int rightdeep = TreeDeep(T->rChlid); 76 deep = leftdeep >= rightdeep ? leftdeep + 1 : rightdeep + 1; 77 } 78 return deep; 79 } 80 81 //二叉树叶子结点个数 82 83 //主函数 84 int main(void) 85 { 86 BiTree T; 87 int str, num = 0; 88 printf("输入第一个结点的值,空格表示没有叶结点:\n"); 89 CreateBiTree(&T); 90 printf("先序遍历二叉树:\n"); 91 TraverseBiTree(T); 92 printf("\n"); 93 printf("中序遍历二叉树:\n"); 94 InOrderBiTree(T); 95 printf("\n"); 96 printf("后序遍历二叉树:\n"); 97 PostOrderBiTree(T); 98 printf("\n"); 99 str = TreeDeep(T); 100 printf("树的深度为:%d", str); 101 printf("\n"); 102 system("pause"); 103 return 0; 104 }
标签:
原文地址:http://www.cnblogs.com/cdoublej/p/5427277.html