标签:
之前在写某个迭代算法的时候,发现算法在某些情况下会出错,后来调试过程中发现,计算过程中,某些理论上大于0的数值会在迭代过程中变为0,最后计算过程中出现了除0,导致结果出错。这篇文章的初始目的就是为了阐明为何某些理论上大于0的数在实际计算中会变为0(下溢),后来顺便将很多人讨论过数据类型转换、运算精度也写进去了。之前的有些博客可能有一些局限性(局限于小数或是其他),这的确是一个不好阐述的话题,因此我从数字信号处理中的量化出发,试图给出一个较为直观的认识。文章可能还有一些问题,还请批评指正。
数字信号处理中的量化指将输入信号从一个大的集合映射到一个的小集合的过程。可以简单的、狭义的理解为将一个连续的量映射到离散的集合上的过程。如下图所示,红色曲线是输入信号,通过3比特量化得到的结果为蓝色曲线。
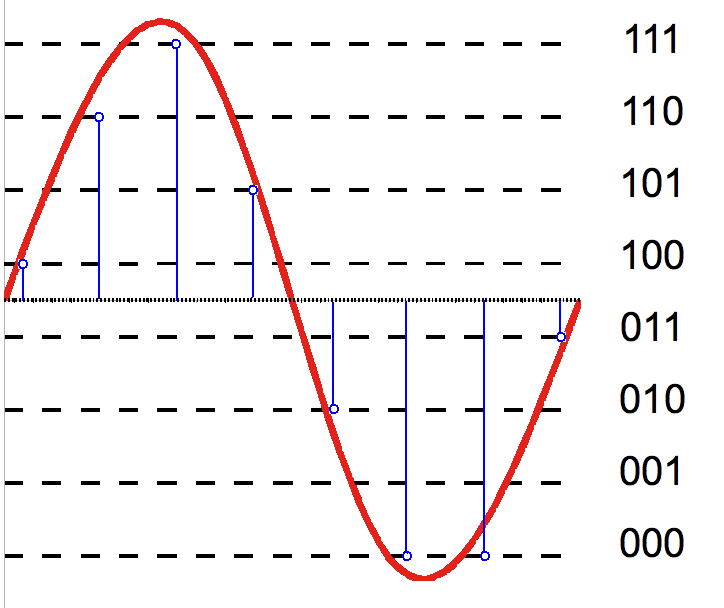
(By Hyacinth - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=30716342)
自然的,可以引出三个问题
为何要将输入信号量化
接收到的信号,譬如通信过程中的电磁波,一般将其视作模拟量(时间上连续,取值连续),为了存储、计算这些信号,需要通过采样、量化将其变为数字量。量化实际上是出于两个考虑,其一是存储、其二是计算。未经量化的信号无法存储在存储器中,同时也无法进行计算。
量化对信号本身有何影响
量化过程中,输入信号的集合往往是不可数的(或者集合有无穷元素),量化输出信号的集合是有限的。这也就意味着量化是一个不可逆的过程,这自然会对信号有影响。如下图所示,量化过程会带来量化噪声(误差,即量化前后信号的差值),即量化后信号会有失真,没有额外先验知识的情况下,失真是无法恢复的。

By Gregory Maxwell - http://wiki.xiph.org/File:Dsat_011.png, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=26171868
如何对输入信号进行量化 (注:此处仅讨论标量量化)
上面的两幅图中,量化是通过将输入范围划分为若干个区域,对于落入同一区域内的信号赋值为同一个(二进制)数。区域的划分是均匀的,这一量化关系可以表示为下图。
不同输入信号取值下,量化误差是相同的,这种方式被称为均匀量化。但是很多情况下,我们更关注相对的量化误差(量化误差/信号取值),即对于小信号而言,量化误差较小,而大信号可以具有相对较大的量化误差。这一情况下可以采用不同的量化方式,如下图所示(注:这是我瞎编的,有对应的非均匀量化的标准)。
非均匀量化可以获得更高的信噪比,两种不同的量化方式具有不同的应用。除此之外还有其他量化方式,此处不再说明。
尽管上节讨论的是数字信号处理中的量化,但是量化、或是类似量化的操作实际上出现在很多地方。譬如计算机的存储空间是有限的,32比特的存储空间仅仅只能够表示种不同的可能。然而很多情况下,我们所期待的运算是在实数域上进行的,而类似数字信号处理中的情况,计算机只能对量化后的信号进行存储和计算。
数据的存储,设计到数据类型,这里讨论两种:整型(integer)和浮点型 (float)。此处,类似量化的思路,我们认为计算机将实数域上的输入,量化为整型/浮点型进行表示。
输入实数域数值,量化范围为
,量化方式为均匀量化,假设
为量化结果,则有
譬如,,则取
。对不同的
,量化误差是一个恒定的取值。
浮点和整型比稍微复杂一些,参考维基百科, 32比特浮点数的存储方式表示如下图。
对应浮点数取值可表示为(十进制) 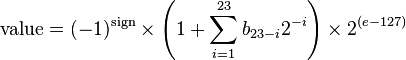
大于0的浮点数依次为,然而大于1的浮点数依次为
,即量化间隔是不同的,实际上,量化精度和数据大小的关系可表示为
即将一个实数域上的数存储为浮点表示,可以看作是一个非均匀量化的过程。
注1:本节中的量化,实际上应该是量化和编码两个过程,不仅仅将数值量化了,同时采用相应的编码方式编码存储。
注2:数据类型的定义比本文描述要复杂,因为设计到0,无穷和非数的处理。
注3:不同运行环境,对于float的定义不尽相同。
类似下面的代码在博客园讨论过很多次了,即
float a = (float) 10.375; float b = (float) 2.263; System.out.println(a+b);
这一代码在我的机器上运行结果输出为12.6380005。虽然鲜有人讨论关于(int) 10.375+ (int) 2.263 = 12这个式子,但是无论是整型还是浮点类型,出现这个问题的缘由都是一样的——我们任意在实数域(或是有理数域)选择了两个数,然而计算机中存储的是量化之后的结果,无论对integer或是float都是这样。只是我们习惯性的认为float强大到无所不能,但是它的表示能力依旧是有限的。
第一节中讨论了量化前后信号的变化,会带来量化噪声。同理,我们给出的数,譬如10.375和2.263,利用浮点存储同样会带来噪声。而计算结果和理论值的差距就是这个噪声的直接体现。
我们并不能够保证,因此计算看似出错了,实际上只是计算机按自己逻辑计算出现的误差。
类似float→double,或是int→long此类的类型转换,或是量化区间增大了,或是量化精度提升了,转化过程不会引发任何问题,简单举例(示意图)。类似这样的量化关系,从int→long→int,或是float→double→float,转化不会进一步引入噪声。
然而如下的转化则不然,即int→float→int
int a = 200000002; float b = (float) a; int c = (int)b; System.out.println(c);
输出结果为200000000;转换过程的示意图可表示为
上溢(Arithmetic overflow),即运算结果超出了寄存器或存储空间所能存储或表示的范围。从量化的角度来看,可以认为是超过了量化范围,上溢一般很容易被发现,但有时也会被忽略。譬如,leetcode的第一题,一个有一些问题的代码也能够通过测试
Given an array of integers, return indices of the two numbers such that they add up to a specific target.
public int[] twoSum(int[] nums, int target) { for (int i = 0; i < nums.length; i++) { for (int j = i + 1; j < nums.length; j++) { if (nums[j] == target - nums[i]) { return new int[] { i, j }; } } } throw new IllegalArgumentException("No two sum solution"); }
上面的代码是提供的解答方式,但是由于nums是int类型的,target也是int类型的,因此target-nums[i]可能会overflow,导致出现错误的结果。
相对而言,“下溢”就隐蔽很多了,下溢(Arithmetic underflow)很难发现,也很不好处理。这里的underflow不是指数据小于所能表示的最小值,这种情况,譬如-129不再int8的表示范围,应该被归类到overflow,即“运算结果超出了寄存器或存储空间所能存储或表示的范围”。
浮点数设计过程中,数据越大,量化精度越低,然而有一个例外,即0附近。32比特浮点数,和0最近的正常数为(不同标准不同),然而比
最接近的数为
。这意味着0附近的量化精度是相对较低的,相对较低的问题并不会带来过多的问题,但是一旦一个非0的数据由于足够小,被存储为0,则可能会带来一系列问题。本来我想举个例子,但是Java里有点怪怪的,我也没弄明白
float a = (float) (1.5*java.lang.Math.pow(10,-45)); float b = Float.MIN_NORMAL; System.out.println(b>a); System.out.println(a); System.out.println(b);
这里我定义了一个a和一个b,b是float中的最小的正常数,然而显然比b小,同时a也大于0,不知道这时怎么处理的。暂时没有查相关资料。
但是不管怎么说,只要一个数足够小,就会被下溢为0,而在迭代算法中,这种情况很有可能会发生。如果不幸这个数被作为了除数,那么就会出现除0的情况,引发错误 。
值得关注的问题是,谈论了那么多关于量化噪声的问题,那么,计算机的计算结果还靠谱吗?即
计算机的计算结果是否能保证绝对的准确性?
在一定条件下是可以的。回到第一节、第二节会发现讨论的前提是
数字信号处理领域,接收信号是模拟的,需要通过ADC采样量化,这时量化噪声是必然存在的。然而,计算机中的数据可能具有不同的含义。譬如,采用变量a表示书本的页数。那么,书本的页数必然是一个不小于0的整数,且一般而言会是有限的。那么,此时若a采用整型存储,就能够精确的表示书本的页数,不引入任何误差。
由此出发,对于不同的应用,如果有一些先验知识,我们有可能可以设计不同的数据类型/结构,以及相应的计算方法,得到准确的计算结果。
标签:
原文地址:http://www.cnblogs.com/sea-wind/p/5436975.html