标签:
最近数值计算学了Guass列主消元法和三角分解法解线性方程组,具体原理如下:
1、Guass列选主元消去法对于AX =B
1)、消元过程:将(A|B)进行变换为 ,其中
,其中 是上三角矩阵。即:
是上三角矩阵。即:

k从1到n-1
a、 列选主元
选取第k列中绝对值最大元素 作为主元。
作为主元。
b、 换行

c、 归一化

d、 消元
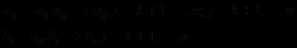
2)、回代过程:由解出。

2、三角分解法(Doolittle分解)
将A分解为如下形式

由矩阵乘法原理
a、计算U的第一行,再计算L的第一列

b、设已求出U的1至r-1行,L的1至r-1列。先计算U的第r行,再计算L的第r列。
a)计算U的r行


b)计算L的r列

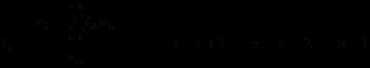
C#代码:
代码说明:Guass列主消元法部分将计算出来的根仍然储存在增广矩阵的最后一列,而Doolittle分解,将分解后的结果也储存至原来的数组中,这样可以节约空间。。
using System;
using System.Windows.Forms;
namespace Test
{
public partial class Form1 : Form
{
public Form1()
{
InitializeComponent();
}
private void Cannel_Button_Click(object sender, EventArgs e)
{
this.textBox1.Clear();
this.textBox2.Clear();
this.textBox3.Clear();
this.comboBox1.SelectedIndex = -1;
}
public double[,] GetNum(string str, int n)
{
string[] strnum = str.Split(‘ ‘);
double[,] a = new double[n, n + 1];
int k = 0;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < strnum.Length / n; j++)
{
a[i, j] = double.Parse((strnum[k]).ToString());
k++;
}
}
return a;
}
public void Gauss(double[,] a, int n)
{
int i, j;
SelectColE(a, n);
for (i = n - 1; i >= 0; i--)
{
for (j = i + 1; j < n; j++)
a[i, n] -= a[i, j] * a[j, n];
a[i, n] /= a[i, i];
}
}
//选择列主元并进行消元
public void SelectColE(double[,] a, int n)
{
int i, j, k, maxRowE;
double temp; //用于记录消元时的因数
for (j = 0; j < n; j++)
{
maxRowE = j;
for (i = j; i < n; i++)
if (System.Math.Abs(a[i, j]) > System.Math.Abs(a[maxRowE, j]))
maxRowE = i;
if (maxRowE != j)
swapRow(a, j, maxRowE, n); //与最大主元所在行交换
//消元
for (i = j + 1; i < n; i++)
{
temp = a[i, j] / a[j, j];
for (k = j; k < n + 1; k++)
a[i, k] -= a[j, k] * temp;
}
}
return;
}
public void swapRow(double[,] a, int m, int maxRowE, int n)
{
int k;
double temp;
for (k = m; k < n + 1; k++)
{
temp = a[m, k];
a[m, k] = a[maxRowE, k];
a[maxRowE, k] = temp;
}
}
public void Doolittle(double[,] a, int n)
{
for (int i = 0; i < n; i++)
{
if (i == 0)
{
for (int j = i + 1; j < n; j++)
a[j, 0] = a[j, 0] / a[0, 0];
}
else
{
double temp = 0, s = 0;
for (int j = i; j < n; j++)
{
for (int k = 0; k < i; k++)
{
temp = temp + a[i, k] * a[k, j];
}
a[i, j] = a[i, j] - temp;
}
for (int j = i + 1; j < n; j++)
{
for (int k = 0; k < i; k++)
{
s = s + a[j, k] * a[k, i];
}
a[j, i] = (a[j, i] - s) / a[i, i];
}
}
}
}
private void Exit_Button_Click(object sender, EventArgs e)
{
this.Close();
}
private void Confirm_Button_Click(object sender, EventArgs e)
{
if (this.textBox2.Text.Trim().ToString().Length == 0)
{
this.textBox2.Text = this.textBox1.Text.Trim();
}
else
{
this.textBox2.Text = this.textBox2.Text + "\r\n" + this.textBox1.Text.Trim();
}
this.textBox1.Clear();
}
private void Calculate_Button_Click(object sender, EventArgs e)
{
string str = this.textBox2.Text.Trim().ToString();
string myString = str.Replace("\n", " ").Replace("\r", string.Empty);
double[,] a = new double[this.textBox2.Lines.GetUpperBound(0) + 1, this.textBox2.Lines.GetUpperBound(0) + 2];
a = GetNum(myString, this.textBox2.Lines.GetUpperBound(0) + 1);
if (this.comboBox1.Text == "Guass列主消元法")
{
Gauss(a, this.textBox2.Lines.GetUpperBound(0) + 1);
for (int i = 0; i < this.textBox2.Lines.GetUpperBound(0) + 1; i++)
{
this.textBox3.Text = this.textBox3.Text + "\r\nX" + (i + 1) + "=" + a[i, this.textBox2.Lines.GetUpperBound(0) + 1];
}
}
else if (this.comboBox1.Text == "Doolittle三角分解法")
{
this.textBox3.Enabled = true;
Doolittle(a, this.textBox2.Lines.GetUpperBound(0) + 1);
this.label3.Text = "分解后的结果:";
this.textBox3.Clear();
this.textBox3.Text += "L矩阵:\r\n";
for (int i = 0; i < this.textBox2.Lines.GetUpperBound(0) + 1; i++)
{
for (int j = 0; j < this.textBox2.Lines.GetUpperBound(0) + 1; j++)
{
if (j < i)
{
this.textBox3.Text += a[i, j].ToString() + "\t";
}
else if (i == j)
{
this.textBox3.Text += "1\t";
}
else
{
this.textBox3.Text += "0\t";
}
}
this.textBox3.Text += "\r\n";
}
this.textBox3.Text += "\r\nU矩阵:\r\n";
for (int i = 0; i < this.textBox2.Lines.GetUpperBound(0) + 1; i++)
{
for (int j = 0; j < this.textBox2.Lines.GetUpperBound(0) + 1; j++)
{
if (j >= i)
{
this.textBox3.Text += a[i, j].ToString() + "\t";
}
else
{
this.textBox3.Text += "0\t";
}
}
this.textBox3.Text += "\r\n";
}
}
}
private void textBox1_KeyDown(object sender, KeyEventArgs e)
{
if (e.KeyCode == Keys.Enter)
{
if (this.textBox1.Text.Trim().ToString().Length == 0)
{
Calculate_Button_Click(sender, e);
}
else
{
Confirm_Button_Click(sender, e);
}
}
}
private void button1_Click(object sender, EventArgs e)
{
this.textBox2.Enabled = true;
}
}
}
运行截图:
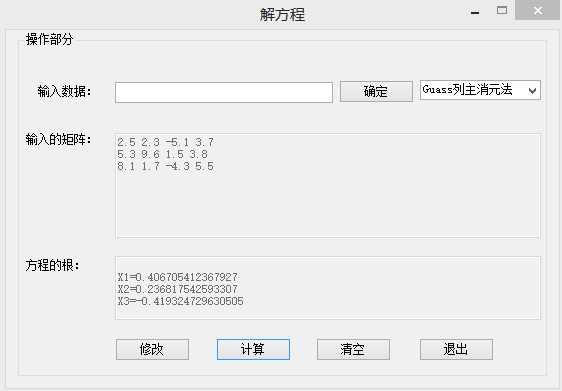
至此完毕。。。。
标签:
原文地址:http://www.cnblogs.com/czx1/p/5438136.html