标签:
Rb树简介
红黑树是一棵二叉搜索树,它在每个节点上增加了一个存储位来表示节点的颜色,可以是Red或Black。通过对任何一条从根到叶子简单 路径上的颜色来约束,红黑树保证最长路径不超过最短路径的两倍,因而近似于平衡。(性质3、性质4保证了红黑树最长的路径不超过最短路径的两倍)
如图所示:
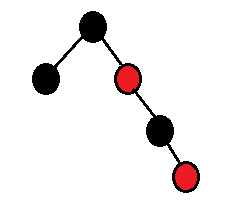
红黑树是满足下面红黑性质的二叉搜索树
1. 每个节点,不是红色就是黑色的
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个子节点是黑色的
4. 对每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点。
好,现在了解了红黑树的特性之后,我们来开始创建红黑树。
//红黑树的节点的结构
1 template<class K,class V> 2 struct RedBlaceTreeNode 3 { 4 typedef RedBlaceTreeNode<K, V> Node; 5 RedBlaceTreeNode(const K& key,const V& value) 6 :_left(NULL), _right(NULL), _parent(NULL) 7 , _key(key), _value(value), _col(RED) 8 {} 9 10 Node* _left; 11 Node* _right; 12 Node* _parent; 13 K _key; 14 V _value; 15 Sign _col; 16 };
//红黑树的结构
template<class K,class V> class RedBlaceTree { typedef RedBlaceTreeNode<K, V> Node; public: RedBlaceTree() :_root(NULL) {} public: bool _Push(const K& key, const V& value); void _LeftSpin(Node*& parent); void _RightSpin(Node*& parent); void _LeftRightSpin(Node*& parent); void _RightLeftSpin(Node*& parent); /*Check*/ //1. 每个节点,不是红色就是黑色的 //2. 根节点是黑色的 //3. 如果一个节点是红色的,则它的两个子节点是黑色的 //4. 对每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点 void _Inorder(){ Inorder(_root); } void Inorder(Node* root); protected: Node* _root; };
//创建红黑树的函数 _Push()
插入的几种情况
cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
1.第一种情况 cur为红,p为红,g为黑,u存在且为红 则将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。( 还挺简单 O(∩_∩)O 继续往下看↓↓)
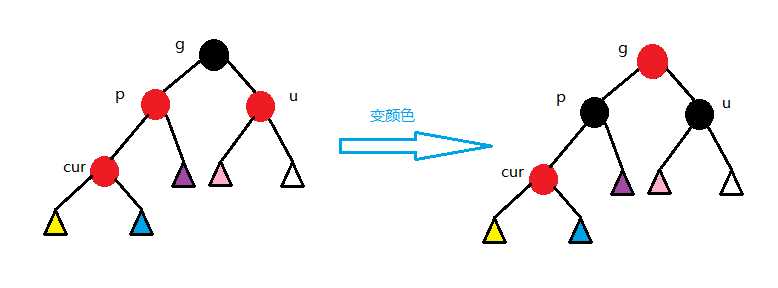
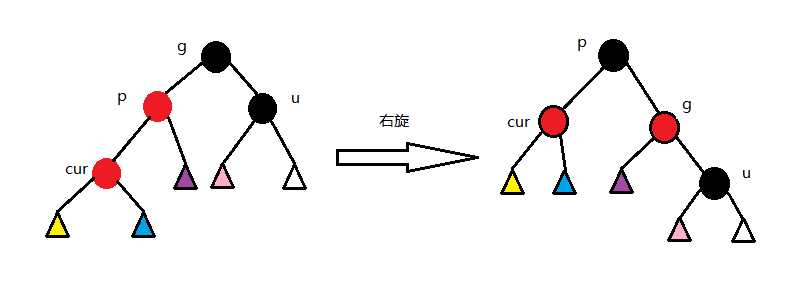
2.第二种情况 cur为红,p为红,g为黑,u不存在/u为黑 p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反,p为g的右孩子,cur为p的右孩子,则进行左单旋转 p、g变色--p变黑,g变红
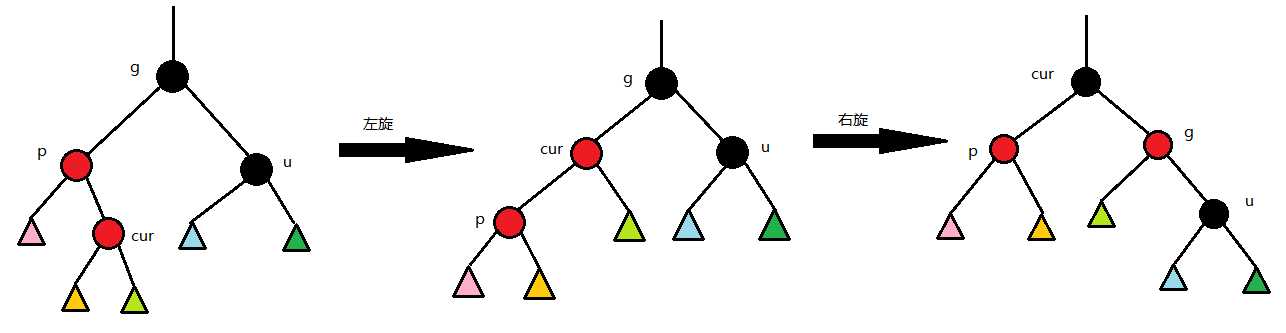
3.第三种情况 cur为红,p为红,g为黑,u不存在/u为黑
p为g的左孩子,cur为p的右孩子,则针对p做左单旋转;相反,p为g的右孩子,cur为p的左孩子,则针对p做右单旋转 则转换成了情况2
template<class K, class V> bool RedBlaceTree<K, V>::_Push(const K& key, const V& value) { Node* cur = _root; Node* parent = NULL; if (_root == NULL) { _root = new Node(key, value); _root->_col = BLACK; } else { while (cur) { parent = cur; if (key > cur->_key) { cur = cur->_right; } else if (key < cur->_key) { cur = cur->_left; } else { return false; } } cur = new Node(key, value); if (key > parent->_key) { parent->_right = cur; cur->_parent = parent; } else { parent->_left = cur; cur->_parent = parent; } if (parent->_col == RED) //如果父亲节点为红色就需要调整 { bool sign = false; //标记位,用来标记grandparent是否为根节点 while (cur->_parent) { Node* grandparent = NULL; Node* uncle = NULL; parent = cur->_parent; grandparent = parent->_parent; if (grandparent) //如果祖父节点存在 { if (grandparent == _root) { sign = true; //标记祖父节点是否为根节点 } if (parent->_key > grandparent->_key) //确定叔父节点 { uncle = grandparent->_left; } else { uncle = grandparent->_right; } //第一种情况:cur为红,p为红,g为黑,u存在且为红 if (uncle && uncle->_col == RED) { parent->_col = BLACK; uncle->_col = BLACK; grandparent->_col = RED; if (sign) { break; } cur = grandparent; } //第二种情况:cur为红,p为红,g为黑,u不存在/u为黑(单旋) //第三种情况:cur为红,p为红,g为黑,u不存在/u为黑(双旋) else { //第二 if (grandparent->_left == parent && parent->_left == cur) { grandparent->_col = RED; parent->_col = BLACK; _RightSpin(grandparent); if (sign) { _root = grandparent; } break; } else if (grandparent->_right == parent && parent->_right == cur) { grandparent->_col = RED; parent->_col = BLACK; _LeftSpin(grandparent); if (sign) { _root = grandparent; } break; } //第三 else if (grandparent->_left == parent && parent->_right == cur) { grandparent->_col = RED; cur->_col = BLACK; _LeftRightSpin(grandparent); if (sign) { _root = grandparent; } break; } else if (grandparent->_right == parent && parent->_left == cur) { grandparent->_col = RED; cur->_col = BLACK; _RightLeftSpin(grandparent); if (sign) { _root = grandparent; } break; } } } else //cur 的上面只有一层 { break; } } } } _root->_col = BLACK; }
标签:
原文地址:http://www.cnblogs.com/shihaokiss/p/5440999.html