直方图均衡

标签：

直方图均衡化的目的是为了找到并应用一个点运算使得修正后图像的直方图近似于一个均匀分布。基本思想是对于一幅图像（原始直方图为h）找到并应用一种点运算，使得修正后的图像的直方图h_eq近似均匀分布，因此累计直方图H_eq应该近似楔形。由于直方图是一个离散分布，均匀点运算只能移动和合并直方图条目，所以只能在整体上得到一个近似的解。

       根据以上变换思想，所求的点运算可以从原始图像的累积直方图H中求得：

其中图像大小为M×N，像素取值范围为[0，K-1]。用Matlab实现的代码如下所示：

%%

I = imread(‘Fig0316.tif‘);

subplot(231);imshow(I);title(‘原图像‘);

[m,n] = size(I);

H = zeros(1,256);

for v=1:m

    for u =1:n

        a = I(v,u);

        H(a+1) = H(a+1)+1;   %求原图像的直方图    

    end              

end

subplot(232);plot(1:256,H);title(‘原图像的直方图‘);

for k=2:256

    H(k) = H(k)+H(k-1);     %求原图像的累积直方图

end

subplot(233);plot(1:256,H);title(‘原图像的累积直方图‘);

H2 = zeros(1,256);

for v=1:m

    for u =1:n

    %直方图均衡化操作

    %原理是均匀分布图像的累积直方图是一个线性斜坡形状（楔形）

    %基本思想是通过变换把原图像的累积直方图变为近似楔形

    a = I(v,u);

    b = uint8(H(a+1)*255/(m*n));  %其中m*n是图像大小，灰度范围是0~255

    I(v,u) = b;

    H2(b+1) = H2(b+1)+1;

    end              

end

subplot(234);imshow(I);title(‘直方图均衡后的图像‘);

subplot(235);plot(1:256,H2);title(‘直方图均衡后图像的直方图‘);

for k=2:256

    H2(k) = H2(k)+H2(k-1);

end

subplot(236);plot(1:256,H2);title(‘直方图均衡后图像的累积直方图‘);

%%

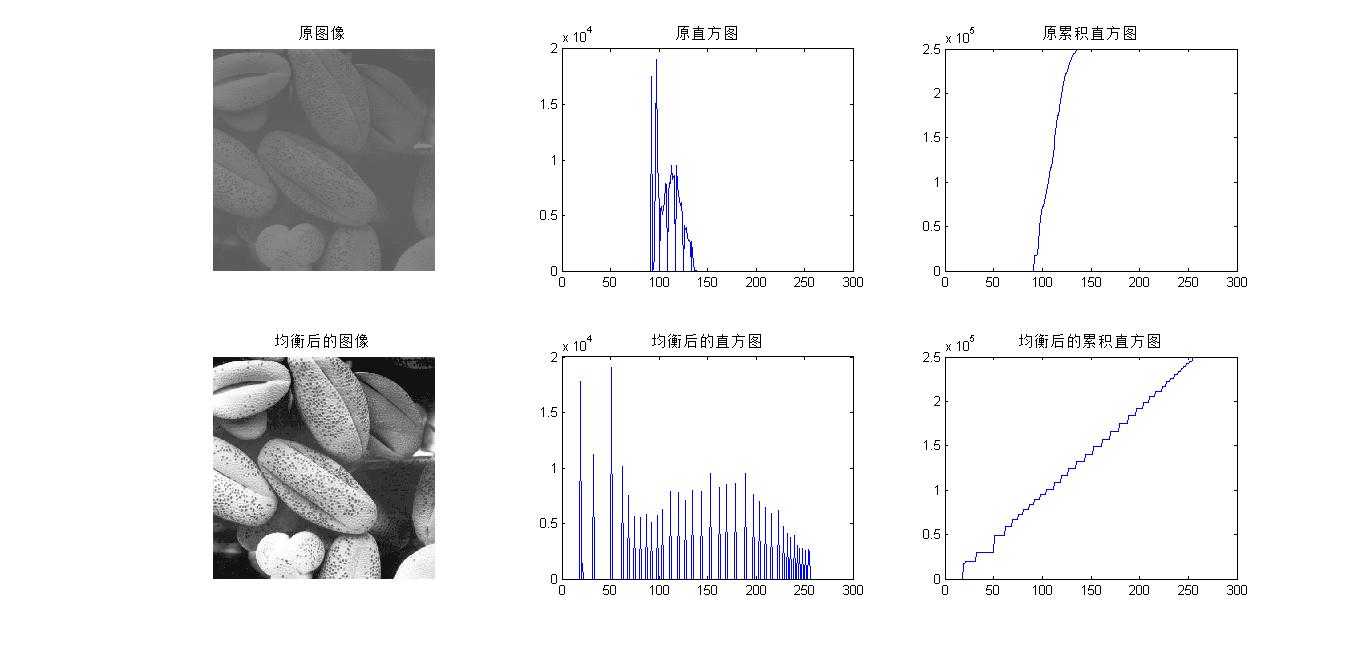
仿真结果如下图所示：

直方图均衡

标签：

原文地址：http://www.cnblogs.com/FlyingFlyer/p/5451196.html