标签:
题目:输入一棵二叉树和一个整数,打印出二叉树中结点值的和为输入整数的所有路径.从树的根结点开始往下一直到叶结点所经过的结点形成一条路径.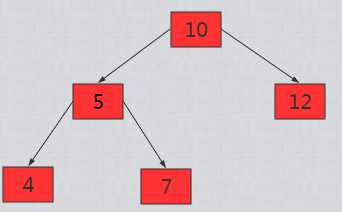
二叉树中有两条和为22的路径:一条路径经过结点10,5,7,另一条路径经过结点10,12
我们接着要遍历其他的结点.在遍历下一个结点之前,先要从结点4回到结点5,再去遍历结点5和右子节点7。值得注意的是,回到结点5的时候,由于结点4已经不在前往结点7的路径上,我们需要把结点4从路径中删除.接下来访问到结点7的时候,再把该结点添加到路径中.此时路径中三个结点10,5,7之和刚好是22,是一条符合要求的路径.
遍历图中二叉树的过程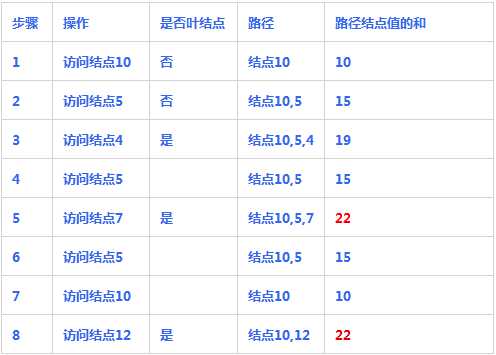
分析完前面具体的例子之后,我们就找到了一些规律。当用前序遍历的方式访问某一结点时,我们把该结点添加到路径上,并累加该结点的值.如果该结点为叶结点并且路径中结点值的和刚好等于输入的整数,则当前的路径符合要求,我们把它打印出来。如果当前结点不是叶结点,则继续访问它的子结点.当访问结束后,递归函数将自动回到它的父结点。因此我们在函数退出之前要在路径上删除当前结点并减去当前结点的值,以确保返回父结点时路径刚好从根结点到父结点的路径。我们不难看出保存路径的数据结构实际上就是一个栈,因为路径要与递归调用状态一致,而递归调用的本质就是一个压栈和出栈的过程。
1 void FindPath(BinaryTreeNode* pRoot,int expectedSum) 2 { 3 if(pRoot==NULL) 4 return; 5 std::vector<int> path; 6 int currentSum=0; 7 FindPath(pRoot,expectedSum,path,currentSum); 8 } 9 10 void FindPath 11 ( 12 BinaryTreeNode* pRoot, 13 int expectedSum, 14 std::vector<int>& path, 15 int currentSum 16 ) 17 { 18 currentSum +=pRoot->value; 19 path.push_back(pRoot->value); 20 //如果是叶结点,并且路径上结点的和等于输入的值,打印出这条路径 21 bool isLeaf =(pRoot->lchild==NULL&&pRoot->rchild==NULL); 22 if(currentSum==expectedSum&&isLeaf) 23 { 24 printf("A path is found:"); 25 std::vector<int>::iterator iter=path.begin(); 26 for(;iter!=path.end();++iter) 27 printf("%d\t",*iter); 28 printf("\n"); 29 } 30 //如果不是叶结点,则遍历它的子结点 31 if(pRoot->lchild!=NULL) 32 FindPath(pRoot->lchild,exception,path,currentSum); 33 if(pRoot->rchild!=NULL) 34 FindPath(pRoot->rchild,expection,path,currentSum); 35 36 //在返回父结点之前,在路径上删除当前结点 37 path.pop_back(); 38 } 39
标签:
原文地址:http://www.cnblogs.com/wxdjss/p/5452521.html