In the ceiling in the basement of a newly open developers building a light source has been installed. Unfortunately, the material used to cover the floor is very sensitive to light. It turned out that its expected life time is decreasing dramatically. To avoid this, authorities have decided to protect light sensitive areas from strong light by covering them. The solution was not very easy because, as it is common, in the basement there are different pipelines under the ceiling and the authorities want to install the covers just on those parts of the floor that are not shielded from the light by pipes. To cope with the situation, the first decision was to simplify the real situation and, instead of solving the problem in 3D space, to construct a 2D model first.
Within this model, the x-axis has been aligned with the level of the
floor. The light is considered to be a point light source with integer
co-ordinates [bx,by]. The pipes are represented by circles. The center
of the circle i has the integer co-ordinates [cxi,cyi] and an integer
radius ri. As pipes are made from solid material, circles cannot
overlap. Pipes cannot reflect the light and the light cannot go through
the pipes. You have to write a program which will determine the
non-overlapping intervals on the x-axis where there is, due to the
pipes, no light from the light source.
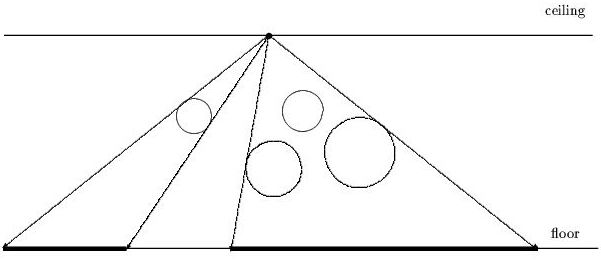
The
input consists of blocks of lines, each of which except the last
describes one situation in the basement. The first line of each block
contains a positive integer number N < 500 expressing the number of
pipes. The second line of the block contains two integers bx and by
separated by one space. Each of the next N lines of the block contains
integers cxi, cyi and ri, where cyi + ri < by. Integers in individual
lines are separated by one space. The last block consists of one line
containing n = 0.
The
output consists of blocks of lines, corresponding to the blocks in the
input(except the last one). One empty line must be put after each block
in the output. Each of the individual lines of the blocks in the output
will contain two real numbers, the endpoints of the interval where there
is no light from the given point light source. The reals are exact to
two decimal places and separated by one space. The intervals are sorted
according to increasing x-coordinate.
#include <iostream>
#include <cstdio>
#include <cstring>
#include <math.h>
#include <algorithm>
#include <stdlib.h>
using namespace std;
const int N = 505;
struct Point {
double x,y,r;
}p[N],p0;
struct Line{
double l,r;
}line[N];
double dis(Point a,Point b){
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
int cmp(Line a,Line b){
if(a.l<b.l) return 1;
return 0;
}
int main()
{
int n;
while(scanf("%d",&n)!=EOF,n){
scanf("%lf%lf",&p0.x,&p0.y);
double angle1,angle2;
for(int i=0;i<n;i++){
scanf("%lf%lf%lf",&p[i].x,&p[i].y,&p[i].r);
double l = dis(p[i],p0); ///p0到圆心的距离
angle1 = asin(p[i].r/l);
double len = (p0.x-p[i].x);///这里千万不能够取绝对值..因为后面的有可能是加
angle2 = asin(len/l);
line[i].l = p0.x - p0.y*tan(angle1+angle2);
line[i].r = p0.x - p0.y*tan(angle2-angle1);
}
sort(line,line+n,cmp);
/*for(int i=0;i<n;i++){
printf("%lf %lf\n",line[i].l,line[i].r);
}*/
double l = line[0].l,r = line[0].r;
for(int i=1;i<n;i++){
if(line[i].l>r){
printf("%.2lf %.2lf\n",l,r);
l = line[i].l;
r = line[i].r;
}
else{
r = max(line[i].r,r);
}
}
printf("%.2lf %.2lf\n\n",l,r);
}
return 0;
}

大概看这个图就能够解除来了。。