标签:
特点
1、二叉树的每个结点至多只有二棵子树(不存在度大于2的结点);
2、在非空二叉树的k层上,至多有2^(k-1)个节点(k>0);
3、高度为k的二叉树中,最多有2^k-1个节点(k>0);
4、对于任何一棵非空的二叉树,如果叶节点个数为n0,度数为2的节点个数为n2,则有: n0 = n2 + 1。
注:通过网上学习得知,国外的教材对于数的高度和深度通常都是从0开始,而国内比较偏向从1开始,所以要注意这个概念上的定义,例如我上文定义的(K>1)。
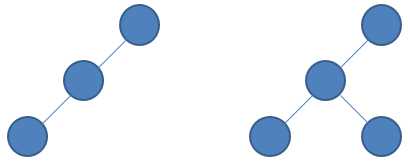 (从二叉树特点判断,以上二图中的树都为二叉树)
(从二叉树特点判断,以上二图中的树都为二叉树)
满二叉树
满二叉树是二叉树的一种,除了具备二叉树的特征,还需要满足的条件是:若一棵深度为k,且有2^k-1个节点称之为满二叉树。就是一个挂满节点的二叉树,叫满二叉树,如下图:
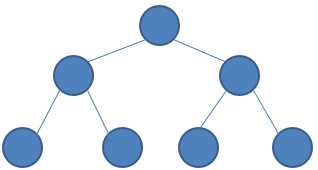
以上二叉树为满二叉树,其中深度K=3,总节点数为2^3-1 = 7。
完全二叉树
除基本二叉树特点外,还需要满足的条件是除最后一层外,每一层上的节点数均达到最大值;在最后一层上只缺少右边的若干结点。换句话说,叶子结点只可能在最大的两层上出现,对任意结点,若其右分支下的子孙最大层次为L,则其左分支下的子孙的最大层次必为L 或 L+1;
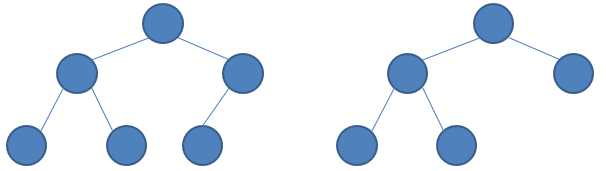
(从完全二叉树特点判断,以上二图中的树都为完全二叉树)
由于二叉树的特点可以得出:
1、满二叉树是一颗挂满节点的数,所以满二叉树一定是完全二叉树,而完全二叉树不一定是满二叉树。
2、根据公式进行推导,假设n0是度为0的结点总数(即叶子结点数),n1是度为1的结点总数,n2是度为2的结点总数,由二叉树的性质可知:n0=n2+1,则n= n0+n1+n2(其中n为完全二叉树的结点总数),由上述公式把n2消去得:n= 2n0+n1-1,由于完全二叉树中度为1的结点数只有0或1两种可能,由此得到n0=(n+1)/2或n0=n/2。总结起来,就是 n0=[n/2],其中[]表示上取整。如上图左边的完全二叉树,n = 6;得知n0 = [6/2] = 3;右边的同理,n0 = [5/2] = 3。
二叉树的实现练习
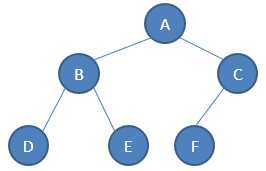
对树的基本运算操作有获取树的高度、获取树的节点数、获取节点的双亲节点和对树遍历,其中,遍历二叉树 是指以一定的次序访问二叉树中的每个结点,遍历二叉树的过程实质是把二叉树的结点进行线性排列的过程,那么遍历的结果得到一个线性序列。从二叉树的递归定义可知,一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此,在任一给定结点上,可以按某种次序执行三个操作:
(1)访问结点本身(N),
(2)遍历该结点的左子树(L),
(3)遍历该结点的右子树(R)。
以上三种操作有六种执行次序:NLR、LNR、LRN、NRL、RNL、RLN。因为前三种次序与后三种次序对称,故只需要讨论先左后右的前三种次序并加以解析。NLR、LNR和LRN分别又称为先根遍历(前序遍历DLR)、中根遍历(中序遍历LDR)和后根遍历(后续遍历LRD)。
前序遍历:ABDECF
前序遍历首先访问根结点然后遍历左子树,最后遍历右子树。在遍历左、右子树时,仍然先访问根结点,然后遍历左子树,最后遍历右子树。
中序遍历:DBEAFC
中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。在遍历左、右子树时,仍然先遍历左子树,再访问根结点,最后遍历右子树。
后序遍历:DEBFCA
后序遍历首先遍历左子树,然后遍历右子树,最后访问根结点,在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后遍历根结点。
Java实现例子
1 public class BinaryTree {
2
3 private TreeNode root=null;
4
5 /**
6 * 创建一棵二叉树
7 * A
8 * B C
9 * D E F
10 */
11 public void createBinTree(){
12 TreeNode root_A = new TreeNode("A");
13 TreeNode node_B = new TreeNode("B");
14 TreeNode node_C = new TreeNode("C");
15 TreeNode node_D = new TreeNode("D");
16 TreeNode node_E = new TreeNode("E");
17 TreeNode node_F = new TreeNode("F");
18 root = root_A;
19 root.leftChild=node_B;
20 root.rightChild=node_C;
21 root.leftChild.leftChild=node_D;
22 root.leftChild.rightChild=node_E;
23 root.rightChild.rightChild=node_F;
24 }
25
26 /**
27 * 获取树的高度
28 * @param subTree
29 * @return
30 */
31 private int height(TreeNode subTree){
32 if(subTree==null)
33 return 0;//递归结束:空树高度为0
34 else{
35 int i=height(subTree.leftChild);
36 int j=height(subTree.rightChild);
37 return (i<j)?(j+1):(i+1);
38 }
39 }
40
41 /**
42 * 获取数的节点数
43 * @param subTree
44 * @return
45 */
46 private int size(TreeNode subTree){
47 if(subTree==null){
48 return 0;
49 }else{
50 return 1+size(subTree.leftChild)+size(subTree.rightChild);
51 }
52 }
53
54 /**
55 * 获取节点的双亲节点
56 * @param element
57 * @return
58 */
59 public TreeNode parent(TreeNode element){
60 return (root==null|| root==element)?null:parent(root, element);
61 }
62
63 public TreeNode parent(TreeNode subTree,TreeNode element){
64 if(subTree==null)
65 return null;
66 if(subTree.leftChild==element||subTree.rightChild==element)
67 //返回父结点地址
68 return subTree;
69 TreeNode p;
70 //现在左子树中找,如果左子树中没有找到,才到右子树去找
71 if((p=parent(subTree.leftChild, element))!=null)
72 //递归在左子树中搜索
73 return p;
74 else
75 //递归在右子树中搜索
76 return parent(subTree.rightChild, element);
77 }
78
79 //前序遍历
80 public void preOrder(TreeNode subTree){
81 if(subTree!=null){
82 visted(subTree);
83 preOrder(subTree.leftChild);
84 preOrder(subTree.rightChild);
85 }
86 }
87
88 //中序遍历
89 public void inOrder(TreeNode subTree){
90 if(subTree!=null){
91 inOrder(subTree.leftChild);
92 visted(subTree);
93 inOrder(subTree.rightChild);
94 }
95 }
96
97 //后续遍历
98 public void postOrder(TreeNode subTree) {
99 if (subTree != null) {
100 postOrder(subTree.leftChild);
101 postOrder(subTree.rightChild);
102 visted(subTree);
103 }
104 }
105
106 public void visted(TreeNode subTree){
107 System.out.print(subTree.data);
108 }
109
110 /**
111 * 二叉树的节点数据结构
112 */
113 private class TreeNode{
114
115 private String data=null;
116 private TreeNode leftChild=null;
117 private TreeNode rightChild=null;
118
119 public TreeNode(){}
120
121 public TreeNode(String data){
122 this.data=data;
123 }
124 }
125
126 public static void main(String[] args) {
127 BinaryTree bt = new BinaryTree();
128 bt.createBinTree();
129 System.out.println("tree height:"+bt.height(bt.root));
130 bt.preOrder(bt.root);
131 System.out.println("---前序遍历");
132 bt.inOrder(bt.root);
133 System.out.println("---中序遍历");
134 bt.postOrder(bt.root);
135 System.out.println("---后序遍历");
136 }
137 }
执行结果:
tree height:3
ABDECF---前序遍历
DBEAFC---中序遍历
DEBFCA---后序遍历
标签:
原文地址:http://www.cnblogs.com/wcd144140/p/5454364.html