标签:
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 4955 | Accepted: 2624 |
Description
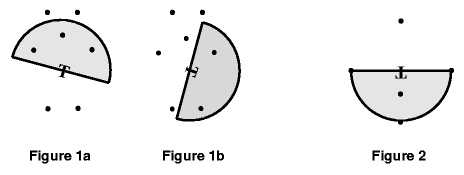
Input
Output
Sample Input
25 25 3.5 7 25 28 23 27 27 27 24 23 26 23 24 29 26 29 350 200 2.0 5 350 202 350 199 350 198 348 200 352 200 995 995 10.0 4 1000 1000 999 998 990 992 1000 999 100 100 -2.5
Sample Output
3 4 4
题意:半圆围绕圆心旋转能够覆盖平面内最多的点
题解:先去掉所有和圆心距离大于r的点,然后我们以每一点和圆心组成的线段为边界来计算线段两边的点,比较出最大值就好了.记得赋值最大值的时候要赋值为0,因为它有可能不会进循环。
#include<stdio.h> #include<iostream> #include<string.h> #include <stdlib.h> #include<math.h> #include<algorithm> using namespace std; const int N = 160; const double eps = 1e-8; struct Point{ double x,y; }p[N],circle; struct Line{ Point a,b; }line; double r; int n; int cross(Point a,Point b,Point c){ double ans = (a.x-c.x)*(b.y-c.y)-(b.x-c.x)*(a.y-c.y); if(fabs(ans)<eps) return 0; if(ans<0) return 1; return -1; } int main(){ while(true){ scanf("%lf%lf%lf",&circle.x,&circle.y,&r); if(r<=0) break; scanf("%d",&n); int k = 0; for(int i=0;i<n;i++){ double x,y; scanf("%lf%lf",&x,&y); if((x-circle.x)*(x-circle.x)+(y-circle.y)*(y-circle.y)>r*r) continue; p[k].x = x; p[k++].y = y; } int temp1 ,temp2,mx = 0; ///mx要赋值为0,因为有可能一个点都没有,习惯赋值成-1被坑了一把 for(int i=0;i<k;i++){ line.a = p[i]; line.b = circle; temp1=temp2 =0; for(int j=0;j<k;j++){ if(cross(p[j],line.a,line.b)==0) { temp1++; temp2++; }else if(cross(p[j],line.a,line.b)==1){ temp1++; }else temp2++; } int ans = max(temp1,temp2); mx = max(ans,mx); } printf("%d\n",mx); } return 0; }
标签:
原文地址:http://www.cnblogs.com/liyinggang/p/5456444.html