标签：

1、二叉树概念

    这里，得先明白树的概念

     摘自：维基百科

在计算机科学中，树（英语：tree）是一种抽象资料型别（ADT）或是实作这种抽象资料型别的数据结构，用来模拟具树状结构性质的资料集合。它是由n（n>=1）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点：

• 每个节点有零个或多个子节点；
• 没有父节点的节点称为根节点；
• 每一个非根节点有且只有一个父节点；
• 除了根节点外，每个子节点可以分为多个不相交的子树；

    摘自：维基百科

二叉树（英语：Binary tree）是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

二叉树的每个节点至多只有二棵子树(不存在度大于2的节点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有个结点；深度为k的二叉树至多共有个结点；对任何一棵二叉树T，如果其终端结点数为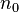，度为2的节点数为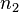，则。

一棵深度为k，且有个节点称之为满二叉树；深度为k，有n个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中，序号为1至n的节点对应时，称之为完全二叉树。

与树不同，树的节点个数至少为1，而二叉树的节点个数可以为0；树中节点的最大度数没有限制，而二叉树节点的最大度数为2；树的节点无左、右之分，而二叉树的结点有左、右之分。

2、特殊说明

      二叉树的遍历，分为：先序遍历、中序遍历、后序遍历，层次遍历

      -------  注意  ----- 

      A、这里的先序、中序、后序，既然说到顺序，那么肯定有个参考点，对吧。 二叉树中的先序、中序、后序选择的参考点是：根节点。选择根为参考点，一定要记住。

      B、先序、中序、后序中，无论哪种，一定要将树从最上面的根节点分成左子树和右子树， 然后再按照各自遍历顺序进行遍历整棵树。

     先序：首先遍历根节点，紧接着遍历左子树，然后才是右子树。

     中序：首先遍历左子树、紧接着遍历根节点、最后遍历右子树。

     后序：首先遍历左子树，紧接着遍历右子树、最后遍历根节点。      

     层次遍历：从上到下、从左到右依次访问每个结点。

3、遍历举例

      A

     B

4、源码实现构建和遍历

   这里的遍历：不包含层次遍历

#include <iostream>
using namespace std;


/// 构建结点
struct BinTreeNode
{
	int index;
	BinTreeNode *lchild;
	BinTreeNode *rchild;
};

/// 构建二叉树
BinTreeNode *create(BinTreeNode *T)
{
	int input;
	cout << "请输入数据:";
	cin >> input;
	if (0 == input)
	{
		T = NULL;
		return T;
	}
	T = (BinTreeNode *)malloc(sizeof(BinTreeNode));
	if (NULL == T)
	{
		cout << " 内存分配出错" << endl;
		exit(1);
	}
	T->index = input;
	T->lchild = create(T->lchild);
	T->rchild = create(T->rchild);

	return  T;
}

/// 先序遍历
void PreOrder(BinTreeNode *T)
{
	if (NULL != T)
	{
		cout << T->index << " ";
		PreOrder(T->lchild);
		PreOrder(T->rchild);
	}
}


/// 中序遍历
void InOrder(BinTreeNode *T)
{
	if (NULL != T)
	{
		InOrder(T->lchild);
		cout << T->index << " ";
		InOrder(T->rchild);
	}
}

/// 后序遍历
void PostOrder(BinTreeNode *T)
{
	if (NULL != T)
	{
		PostOrder(T->lchild);
		PostOrder(T->rchild);
		cout << T->index << " ";
	}
}

int main()
{
	BinTreeNode *T = NULL ;
	T = create(T);
	if (NULL == T)
	{
		cout << "T = NULL" << endl;
		exit(1);
	}

	cout << "先序遍历" << endl;
	PreOrder(T);
	
	cout  << endl << "中序遍历" << endl;
	InOrder(T);

	cout << endl << "后序遍历" << endl;
	PostOrder(T);

	cout << endl;
	system("pause");
	return 0;
}

数据结构之二叉树的递归建立和遍历

标签：

原文地址：http://blog.csdn.net/hk_5788/article/details/51326191