并查集

标签：

并查集（Union-find Sets）是一种非常精巧而实用的数据结构，它主要用于处理一些不相交集合的合并问题。一些常见的用途有求连通子图、求最小生成树的 Kruskal 算法和求最近公共祖先（Least Common Ancestors, LCA）等。

使用并查集时，首先会存在一组不相交的动态集合 S={S1,S2,?,Sk}S={S1,S2,?,Sk}，一般都会使用一个整数表示集合中的一个元素。

每个集合可能包含一个或多个元素，并选出集合中的某个元素作为代表。每个集合中具体包含了哪些元素是不关心的，具体选择哪个元素作为代表一般也是不关心的。我们关心的是，对于给定的元素，可以很快的找到这个元素所在的集合（的代表），以及合并两个元素所在的集合，而且这些操作的时间复杂度都是常数级的。

并查集的基本操作有三个：

1. makeSet(s)：建立一个新的并查集，其中包含 s 个单元素集合。
2. unionSet(x, y)：把元素 x 和元素 y 所在的集合合并，要求 x 和 y 所在的集合不相交，如果相交则不合并。
3. find(x)：找到元素 x 所在的集合的代表，该操作也可以用于判断两个元素是否位于同一个集合，只要将它们各自的代表比较一下就可以了。

并查集的实现原理也比较简单，就是使用树来表示集合，树的每个节点就表示集合中的一个元素，树根对应的元素就是该集合的代表，如图 1 所示。

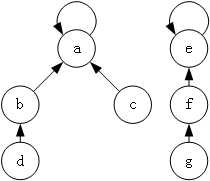
树的节点表示集合中的元素，指针表示指向父节点的指针，根节点的指针指向自己，表示其没有父节点。沿着每个节点的父节点不断向上查找，最终就可以找到该树的根节点，即该集合的代表元素。

现在，应该可以很容易的写出 makeSet 和 find 的代码了，假设使用一个足够长的数组来存储树节点（很类似之前讲到的静态链表），那么 makeSet 要做的就是构造出如图 2 的森林，其中每个元素都是一个单元素集合，即父节点是其自身：

相应的代码如下所示，时间复杂度是 O(n)：

1 const int MAXSIZE = 500;
2 int uset[MAXSIZE];
3  
4 void makeSet(int size) {
5     for(int i = 0;i < size;i++) uset[i] = i;
6 }

接下来，就是 find 操作了，如果每次都沿着父节点向上查找，那时间复杂度就是树的高度，完全不可能达到常数级。这里需要应用一种非常简单而有效的策略——路径压缩。

路径压缩，就是在每次查找时，令查找路径上的每个节点都直接指向根节点，如图 3 所示。

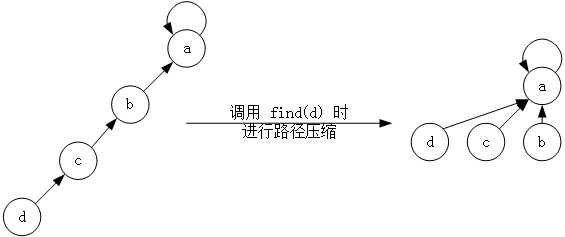
我准备了两个版本的 find 操作实现，分别是递归版和非递归版，不过两个版本目前并没有发现有什么明显的效率差距，所以具体使用哪个完全凭个人喜好了。

 1 int find(int x) {
 2     if (x != uset[x]) uset[x] = find(uset[x]);
 3     return uset[x];
 4 }
 5 int find(int x) {
 6     int p = x, t;
 7     while (uset[p] != p) p = uset[p];
 8     while (x != p) { t = uset[x]; uset[x] = p; x = t; }
 9     return x;
10 }

最后是合并操作 unionSet，并查集的合并也非常简单，就是将一个集合的树根指向另一个集合的树根，如图 4 所示。

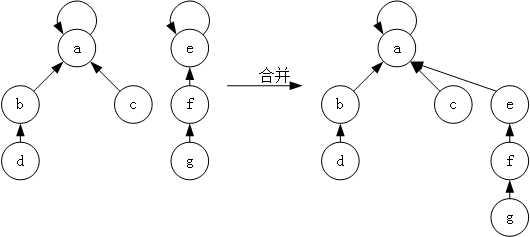
1 void unionSet(int x, int y)
2 {
3     int a=find(x),b=find(y);
4     if(a!=b)
5         uset[a]=uset[b];
6 }

 http://blog.csdn.net/dellaserss/article/details/7724401 精辟

并查集

标签：

原文地址：http://www.cnblogs.com/WDKER/p/5466583.html