标签:style blog http color strong io 数据 for
堆排序,是数据结构中重要的排序方法,可以很快帮你找到最大值。在实际应用中,如 最大优先级队列是大顶推的应用,可以很快找到优先级最高的队列。
1.堆概念
堆的定义如下,n个元素的序列{k1,k2,...kn},当且仅当满足如下关系:
ki>=k2i 或者 ki<=k2i
ki>=k2i+1 ki<=k2i+1
分别对应大顶堆和小顶堆。
堆可以看作一个完全二叉树,所有非终端点都大于或都小于左右孩子,且堆顶数据是最大或最小值。
2.堆排序主要解决问题
堆排序要将无规律的数据排列成一个大顶堆或者小顶堆;如何在删去堆顶后,如何重新调整使它重新变成堆。
3.堆排序
堆排序是反复"筛选"的过程。
在建立堆时,如果将序列看出完全二叉树,那么最好一个非终端点一定【n/2】位置,从该位置开始往前调整。
排序过程,每次用序列最后一个数与堆顶交换,然后对剩下的n-1进行一次调整,依次进行。
4.堆排序代码
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 #define INIT 1000 5 #define INCRENMENT 1000 6 7 8 //顺序列表结构体 9 typedef struct List{ 10 int *elem;//基地址 11 int length;//顺序列表的长度 12 int size;//总长度 13 }List; 14 //列表初始化 15 void init(List &L) 16 { 17 L.elem=(int*)malloc(sizeof(int)*INIT); 18 L.length=0; 19 L.size=INIT; 20 } 21 //显示列表数据 22 void print(List L) 23 { 24 for(int i=1;i<=L.length;i++) 25 printf("%d\t",L.elem[i]); 26 printf("\n"); 27 28 } 29 //插入新数据 30 void insert(List &L,int i) 31 { 32 if(L.length>=L.size) 33 { 34 L.elem=(int*)realloc(L.elem,sizeof(int)*(L.size+INCRENMENT)); 35 if(!L.elem) exit(-1); 36 L.size+=INCRENMENT; 37 } 38 L.elem[++L.length]=i; 39 //printf("%d插入完毕\n",i); 40 41 } 42 //堆调整 本来调整大顶堆 43 void HeapAdjust(List &L,int s,int m) 44 { 45 int temp=L.elem[s]; 46 47 for(int j=2*s;j<=m;j*=2) 48 { 49 if(j<m && L.elem[j]<L.elem[j+1]) j++; 50 if(temp > L.elem[j]) break; 51 L.elem[s]=L.elem[j]; 52 s=j; 53 } 54 55 L.elem[s]=temp; 56 } 57 //堆排序 58 void HeapSort(List &L) 59 { 60 //堆建立 61 for(int i=L.length/2;i>0;i--) 62 { 63 HeapAdjust(L,i,L.length); 64 } 65 66 //堆排序 67 for(int j=L.length;j>0;j--) 68 { //将堆顶和最后一个数据交换 69 int temp=L.elem[j]; 70 L.elem[j]=L.elem[1]; 71 L.elem[1]=temp; 72 HeapAdjust(L,1,j-1); 73 } 74 } 75 int main() 76 { 77 List L; 78 init(L); 79 for(int i=1;i<=10;i++){ 80 insert(L,rand()%1000); 81 } 82 printf("初始化10个随机数据\n"); 83 print(L); 84 HeapSort(L); 85 printf("堆排序后结果\n"); 86 print(L); 87 return 0; 88 }
5.显示结果
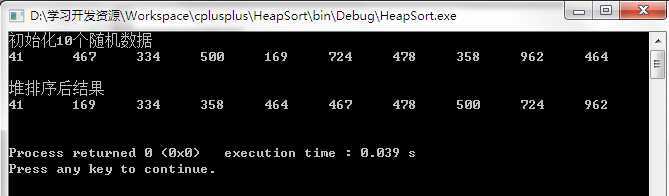
6.堆排序的性能
平均时间O(nlogn) 最差情况O(nlogn)
需要O(1)辅助空间
它在小数据量排序性能不好,但是在大数据量排序性能很明显,比快速排序快。
它是不稳定排序
标签:style blog http color strong io 数据 for
原文地址:http://www.cnblogs.com/forsta/p/3879588.html