poj-1177 Picture（矩形周长并，线段树+扫描线）

标签：

题目链接：点击打开链接

Description

A number of rectangular posters, photographs and other pictures of the same shape are pasted on a wall. Their sides are all vertical or horizontal. Each rectangle can be partially or totally covered by the others. The length of the boundary of the union of all rectangles is called the perimeter. 

Write a program to calculate the perimeter. An example with 7 rectangles is shown in Figure 1. 

The corresponding boundary is the whole set of line segments drawn in Figure 2. 

The vertices of all rectangles have integer coordinates. 

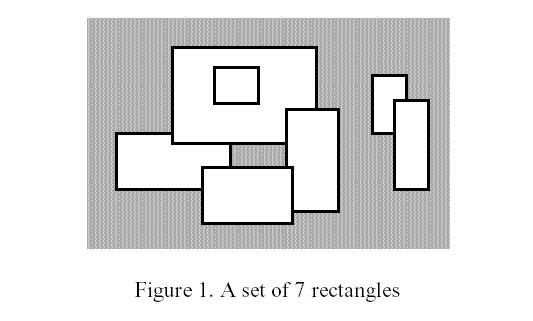
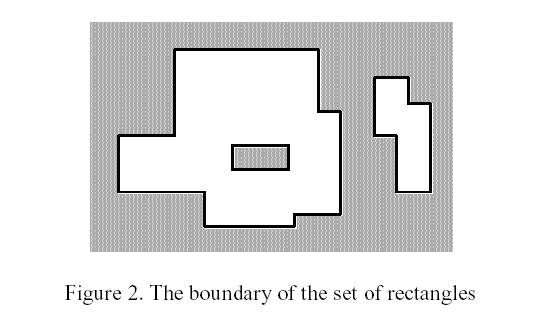
Input

Output

Sample Input

7
-15 0 5 10
-5 8 20 25
15 -4 24 14
0 -6 16 4
2 15 10 22
30 10 36 20
34 0 40 16

Sample Output

228

题意：平面上有很多个矩形，矩形间会相互覆盖，问总的周长是多少。

思路：看到这道题就想到之前做过的矩形面积并，这道题比那道题要多处理一个横边，除此之外就都一样了~ 看了点击打开链接这位大神的思路后豁然开朗。

在之前的矩形面积并模板上改了下AC了，代码的具体打了注释，看代码吧。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define N 10010
struct Node
{
    int l,r;
    int rl,rr;
    int c;///线段的权值，入边为1，出边为-1
    int cnt;///垂直方向有效长度
    int part;///在垂直方向有效段有几个区间，连续的两个区间算一个。
    int isl,isr;///区间左端点和右端点是否被覆盖
}tree[N<<2];
struct Line
{
    int x;
    int y1,y2;
    int c;
} line[N<<1];
int y[N];
bool cmp(Line a,Line b)
{
    if(a.x==b.x)
        return a.c>b.c;///注意不管是poj还是hdu这一步不加都是可以AC的，但是代码却是错的，因为无法判断重边。有重边的情况下，先判断入边再判断出边即可解决。
    return a.x<b.x;
}
void build(int root,int l,int r)
{
    tree[root].l=l;
    tree[root].r=r;
    tree[root].rl=y[l];
    tree[root].rr=y[r];
    tree[root].c=0;
    tree[root].cnt=0;
    tree[root].part=0;
    tree[root].isl=tree[root].isr=0;
    if(l+1==r)
        return;
    int m=(l+r)>>1;
    build(root<<1,l,m);
    build(root<<1|1,m,r);
}
void pushup(int root)
{
    if(tree[root].c>0)
    {
            tree[root].cnt=tree[root].rr-tree[root].rl;
            tree[root].isl=tree[root].isr=1;
            tree[root].part=1;
    }
    else
    {

        if(tree[root].l+1==tree[root].r)
        {
            tree[root].cnt=0;
            tree[root].isl=tree[root].isr=0;
            tree[root].part=0;
        }
        else
        {
            tree[root].cnt=tree[root<<1].cnt+tree[root<<1|1].cnt;
            tree[root].isl=tree[root<<1].isl;
            tree[root].isr=tree[root<<1|1].isr;
            tree[root].part=tree[root<<1].part+tree[root<<1|1].part-tree[root<<1].isr*tree[root<<1|1].isl;
        }
    }
}
void update(int root,Line a)
{
    if(tree[root].rl==a.y1&&tree[root].rr==a.y2)
    {
        tree[root].c+=a.c;
        pushup(root);
        return;
    }
    if(a.y2<=tree[root<<1].rr)
    {
        update(root<<1,a);
    }
    else if(a.y1>=tree[root<<1|1].rl)
    {
        update(root<<1|1,a);
    }
    else
    {
        Line temp=a;
        temp.y2=tree[root<<1].rr;
        update(root<<1,temp);
        temp=a;
        temp.y1=tree[root<<1|1].rl;
        update(root<<1|1,temp);
    }
    pushup(root);
}
int main()
{
    int x1,y1,x2,y2;
    int n;
    int flag=0;
    while(~scanf("%d",&n))
    {
        if(flag==1)
            break;
        int t=1;
        for(int i=0;i<n;i++)
        {
            scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
            line[t].x=x1;
            line[t].y1=y1;
            line[t].y2=y2;
            line[t].c=1;
            y[t++]=y1;
            line[t].x=x2;
            line[t].y1=y1;
            line[t].y2=y2;
            line[t].c=-1;
            y[t++]=y2;
        }///保存每条边和每一个y值
        sort(line+1,line+t,cmp);
        sort(y+1,y+t);
        int num=2;
        for(int i=2;i<t;i++)
            if(y[i]!=y[i-1])
            y[num++]=y[i];///去重
        build(1,1,num-1);
        update(1,line[1]);
        int sum=tree[1].cnt;
        int last_part=tree[1].part;
        int last_cnt=tree[1].cnt;///预处理第一条边，因为后面需要先更新后处理
        for(int i=2;i<t;i++)
        {
            update(1,line[i]);
            sum+=abs(tree[1].cnt-last_cnt);///当新进来一条线段的时候，用更新完的有效长度减去更新前的有效长度即可得出“不是在内部的边的长度”，这点和矩形面积并相反，面积并需要的恰是在内部的边的长度
            sum+=2*last_part*(line[i].x-line[i-1].x);///求出横边，一段（区间）有两条边。注意要用更新之前的part值，应该很容易理解。横边的条数是从左边看到右边的，即我们能确保的只有上一个x到当前x之前的这段距离有更新前的段数*2的边长
            last_part=tree[1].part;
            last_cnt=tree[1].cnt;///滚动
        }
        printf("%d\n",sum);
    }
    return 0;
}

poj-1177 Picture（矩形周长并，线段树+扫描线）

标签：

原文地址：http://blog.csdn.net/acm_cxq/article/details/51330857