标签：
多变量线性回归（Multivariate Linear Regression）
这次的多变量线性回归问题，输入特征向量X是二维的，一个维度表示房间面积，一个维度表示房间数量，输出Y是房子的价格。
这一次试着自己找了一下合适的学习速率和迭代次数
合适的学习速率通过看损失函数J()的下降曲线来判断
其中损失函数这样计算：
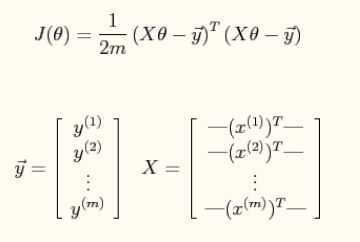合适的损失函数下降曲线该是这样：
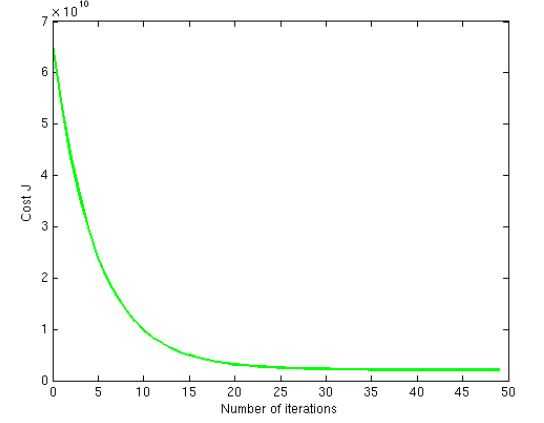
在线法进行迭代的时候，大约200次就会很好的收敛到真值。
而离线法的计算公式为：
可以很精确的计算出回归模型的参数。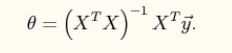
作者多次提醒，在线法计算的时候，需要对各个维度的数据进行归一化，这样大大有利于参数收敛，可以很快的收敛到真值附近。
而离线算法是精确的求解线性方程组，不需要数据预处理，只需要特征向量X拓展一个截距项就行。
但是-------离线算法需要求解矩阵的逆，当数据量较大的时候，这个方法就不适合了。
clc clear all; close all; x = load(‘ex3x.dat‘);%加载数据 y = load(‘ex3y.dat‘); %%%%--------------------数据预处理----------------------%%%%%% m = length(y); x = [ones(m, 1), x]; theta2=(x‘*x)^(-1)*x‘*y;%%%%%%%%%%%%--离线算法计算---%%%%%%%%%% sigma = std(x);%取方差 mu = mean(x);%取均值 x(:,2) = (x(:,2) - mu(2))./ sigma(2);%归一化 x(:,3) = (x(:,3) - mu(3))./ sigma(3);%归一化 theta = zeros(size(x(1,:)))‘; % initialize fitting parameters alpha = 0.08; %% Your initial learning rate %% J = zeros(50, 1); %初始化损失函数 for num_iterations = 1:500 J(num_iterations) = 1/2/m*sum(x*theta-y)^2;%批量梯度下降 theta = theta-alpha./m.*x‘*(x*theta-y);%% 参数更新 end % now plot J % technically, the first J starts at the zero-eth iteration % but Matlab/Octave doesn‘t have a zero index figure; plot(0:49, J(1:50), ‘-‘) xlabel(‘Number of iterations‘) ylabel(‘Cost J‘) x_test=[1,1650,3];%测试样本 y2=x_test*theta2 %------离线算法结果测试 x_test(2) = (x_test(2) - mu(2))./ sigma(2);%归一化 x_test(3) = (x_test(3) - mu(3))./ sigma(3);%归一化 y1=x_test*theta %-------在线迭代算法结果测试
标签：
原文地址：http://www.cnblogs.com/YangQiaoblog/p/5467967.html
