标签:
单调队列优化DP的模板题
不难列出DP方程:
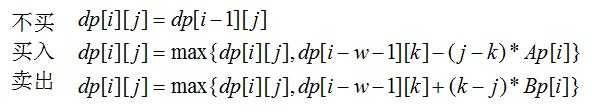
对于买入的情况
由于dp[i][j]=max{dp[i-w-1][k]+k*Ap[i]-j*Ap[i]}
AP[i]*j是固定的,在队列中维护dp[i-w-1][k]+k*Ap[i]的单调性即可
1 #include<stdio.h> 2 #include<string.h> 3 #include<algorithm> 4 using namespace std; 5 const int maxn = 2010; 6 int T,maxP,w,Ap[maxn],Bp[maxn],As[maxn],Bs[maxn],dp[maxn][maxn],q[maxn*10]; 7 8 int main(){ 9 scanf("%d%d%d", &T, &maxP, &w); 10 for (int i=1; i<=T; i++) 11 scanf("%d%d%d%d", &Ap[i], &Bp[i], &As[i], &Bs[i]); 12 memset(dp,-127,sizeof(dp)); 13 for (int i=1; i<=T; i++){ 14 for (int j=0; j<=As[i]; j++) dp[i][j]=-Ap[i]*j; 15 for (int j=0; j<=maxP; j++) dp[i][j]=max(dp[i][j], dp[i-1][j]); 16 if (i-w-1>=0){ 17 int head=0, tail=0; 18 for (int j=0; j<=maxP; j++){ 19 while (head<tail && q[head]+As[i]<j) head++; 20 while (head<tail && dp[i-w-1][j]+j*Ap[i] >= dp[i-w-1][q[tail-1]]+q[tail-1]*Ap[i]) tail--; 21 q[tail++]=j; 22 if (head<tail) dp[i][j]=max(dp[i][j], dp[i-w-1][q[head]]-(j-q[head])*Ap[i]); 23 } 24 head=0, tail=0; 25 for (int j=maxP; j>=0; j--){ 26 while (head<tail && q[head]-Bs[i]>j) head++; 27 while (head<tail && dp[i-w-1][j]+j*Bp[i] >= dp[i-w-1][q[tail-1]]+q[tail-1]*Bp[i]) tail--; 28 q[tail++]=j; 29 if (head<tail) dp[i][j]=max(dp[i][j], dp[i-w-1][q[head]]+(q[head]-j)*Bp[i]); 30 } 31 } 32 } 33 int ans=0; 34 for (int i=0; i<=maxP; i++) 35 ans=max(ans, dp[T][i]); 36 printf("%d\n", ans); 37 return 0; 38 }
bzoj1855: [Scoi2010]股票交易--单调队列优化DP
标签:
原文地址:http://www.cnblogs.com/mzl120918/p/5469164.html