标签:
一,介绍
什么是二项队列,为什么会用到二项队列?
与二叉堆一样,二项队列也是优先级队列的一种实现方式。在 数据结构--堆的实现之深入分析 的末尾 ,简单地比较了一下二叉堆与二项队列。
对于二项队列而言,它可以弥补二叉堆的不足:merge操作的时间复杂度为O(N)。二项队列的merge操作的最坏时间复杂度为O(logN)。
二,二项队列的基本操作及实现
在详细介绍二项的队列的基本操作之前,先了解下二项队列这种数据结构:
1)一个二项队列是若干棵树的集合。也就是说,二项队列不仅仅是一棵树,而是多棵树,并且每一棵树都遵守堆序的性质,所谓堆序的性质,就是指每个结点都比它的左右子树中结点要小(小顶堆)。这棵树称为“二项树”
2)二项队列中的树高度不同,一个高度至多存在一棵二项树。将高度为0的二项树记为 B(0),高度为 k 的二项树记为 B(k)
也就是说,对于k>=0,二项队列中至多存在一棵 B(k)的二项树。
3)B(k)是由 B(0)、B(1)、B(2)....B(k-1)组成的。B(0)是一棵单节点(2^0 = 1)的树,B(k)中含有 2^k 个结点。
高度为 k 的二项树B(k)通过将一棵二项树B(k-1)附到另一棵二项树B(k-1)的根上构成。而B(k-1)又可以由B(k-2)附到另一棵B(k-2)的二项树上,故正如上面提到,B(k)是由 B(0)、B(1)、B(2)....B(k-1)组成的。
4)具有N个结点的二项队列最多有 logN 棵二项树。因为,每棵二项树B(k)中含有2^k个结点。
故:2^0 + 2^1 + 2^2 + .... + 2^k = N,得到 k=logN。k为树的棵数。
注意到上面提到的是“最多” 有logN 棵二项树,这说明一个二项队列可以缺少某棵 B(i) , 0<=i<=k
5)由二项树中结点个数的性质(B(k)有2^k个结点),而二项队列又是若干二项树的集合,故二项队列可以采用二进制数来标记:
如,大小为13(共有13个结点)的二项队列可以用森林 B(3)、B(2)、B(0)表示,并可以把这种表示写成 1101,1101以二进制形式表示13,而且还表示了该二项队列中,不存在B(1)这样的树。
介绍了二项队列的性质或者说逻辑结构,现在介绍下二项队列的存储结构。
二项队列是在内在中如何存储的呢?(从网上找到一张图如下:)

首先是需要一个一维数组。该数组中的每个元素存储一棵二项树的根结点指针。比如,最右边的那个数组元素存储了一颗高度为0的二项树B(0)。B(0)只有一个结点,该结点的权值为13。如果数组的长度表示二进制的位数,那么这个二项队列表示为 00001101
这说明该二项队列不存在高度为7、6、5、4、1 这样的二项树:B(7)、B(6)、B(5)、B(4)、B(1)
此外,还可以看出:
①数组大小为二项树的数目乘2加1,或者说二项树的数目是数组的长度除以2再减去1。二项树在数组中存储是按高度排序的。
②数组第 i 号索引处,存储的是高度为 i 的二项树。如,第0号索引,存储高度为0的二项树,该二项树只有一个结点,结点权值为13
除了需要一维数组外,树的链表表示,这里采用的是“左孩子右兄弟”表示法。
因此,二项队列的实现类的结构如下:
1 public final class BinomialQueue<AnyType extends Comparable<? super AnyType>> 2 { 3 4 private static final int DEFAULT_TREES = 1; 5 6 private int currentSize; // # items in priority queue 7 private BinNode<AnyType> [ ] theTrees; // An array of tree roots 8 9 /** 10 * Construct the binomial queue. 11 */ 12 public BinomialQueue( ) 13 { 14 theTrees = new BinNode[ DEFAULT_TREES ]; 15 makeEmpty( ); 16 } 17 18 19 private static class BinNode<AnyType> 20 { 21 AnyType element; // The data in the node 22 BinNode<AnyType> leftChild; // Left child 23 BinNode<AnyType> nextSibling; // Right child 24 // Constructors 25 BinNode( AnyType theElement ) 26 { 27 this( theElement, null, null ); 28 } 29 30 //other operations..... 31 } 32 //other operations..... 33 }
第7行是一维数组,第19至23行是采用“左孩子右兄弟”表示法的结点的定义。
①merge操作
merge操作是合并二个二项队列,合并二项队列过程中需要合并这两个二项队列中 高度相同的二项树(后面的combineTrees()方法)
假设需要合并二项队列H(1)和H(2),合并后的结果为H(3)。合并两个二项队列的过程如下:
a)寻找H(1)和H(2)中高度相同的二项树,调用combineTrees()合并这两颗二项树
b)重复 a) 直至树中不再有高度相同的二项树为止
代码分析如下:
1 /** 2 * Return the result of merging equal-sized t1 and t2. 3 */ 4 private BinNode<AnyType> combineTrees( BinNode<AnyType> t1, BinNode<AnyType> t2 ) 5 { 6 if( t1.element.compareTo( t2.element ) > 0 ) 7 return combineTrees( t2, t1 );//第一个参数t1总是代表:根的权值较小的那颗二项树 8 t2.nextSibling = t1.leftChild; 9 t1.leftChild = t2; 10 return t1; 11 }
combineTrees()方法用来合并两棵高度相同的二项树,(注意是二项树,而不是二项队列)。树采用的是左孩子右兄弟表示法。
第4行,t1是根的权值较小的二项树树,第8-9行,将根权值较大的那颗二项树成为根权值较小的二项树(t1)的子树,即可完成二项树的合并。
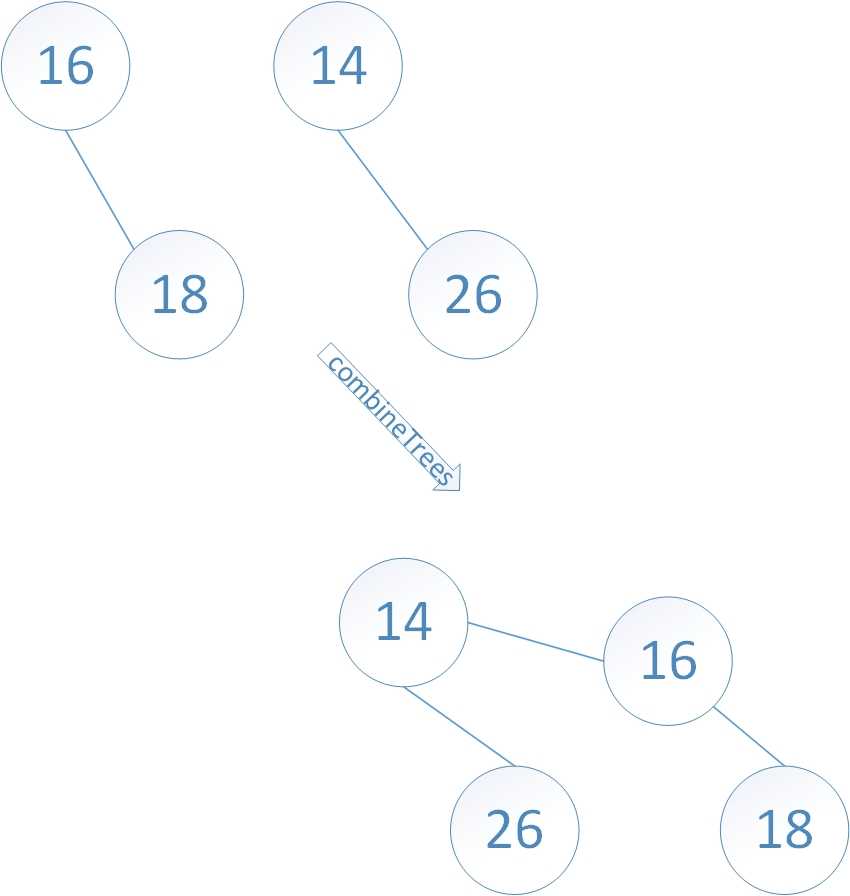
二项队列的合并,是二项队列中高度相同的各个子树之间的合并。
故merge操作的代码如下(来自于《数据结构与算法分析Mark Allen Weiss》):
1 /** 2 * Merge rhs into the priority queue. 合并this 和 rhs 这两个二项队列 3 * rhs becomes empty. rhs must be different from this. 4 * @param rhs the other binomial queue. 5 */ 6 public void merge( BinomialQueue<AnyType> rhs ) 7 { 8 if( this == rhs ) // Avoid aliasing problems.不支持两个相同的二项队列合并 9 return; 10 11 currentSize += rhs.currentSize;//新合并后的二项队列中的结点个数 12 13 if( currentSize > capacity( ) ) 14 { 15 int newNumTrees = Math.max( theTrees.length, rhs.theTrees.length ) + 1; 16 expandTheTrees( newNumTrees ); 17 } 18 19 BinNode<AnyType> carry = null; 20 for( int i = 0, j = 1; j <= currentSize; i++, j *= 2 ) 21 { 22 BinNode<AnyType> t1 = theTrees[ i ]; 23 BinNode<AnyType> t2 = i < rhs.theTrees.length ? rhs.theTrees[ i ] : null; 24 //合并分8种情况 25 int whichCase = t1 == null ? 0 : 1; 26 whichCase += t2 == null ? 0 : 2; 27 whichCase += carry == null ? 0 : 4; 28 29 switch( whichCase ) 30 { 31 case 0: /* No trees */ 32 case 1: /* Only this */ 33 break; 34 case 2: /* Only rhs */ 35 theTrees[ i ] = t2; 36 rhs.theTrees[ i ] = null; 37 break; 38 case 4: /* Only carry */ 39 theTrees[ i ] = carry; 40 carry = null; 41 break; 42 case 3: /* this and rhs */ 43 carry = combineTrees( t1, t2 ); 44 theTrees[ i ] = rhs.theTrees[ i ] = null; 45 break; 46 case 5: /* this and carry */ 47 carry = combineTrees( t1, carry ); 48 theTrees[ i ] = null; 49 break; 50 case 6: /* rhs and carry */ 51 carry = combineTrees( t2, carry ); 52 rhs.theTrees[ i ] = null; 53 break; 54 case 7: /* All three */ 55 theTrees[ i ] = carry; 56 carry = combineTrees( t1, t2 ); 57 rhs.theTrees[ i ] = null; 58 break; 59 } 60 } 61 62 for( int k = 0; k < rhs.theTrees.length; k++ ) 63 rhs.theTrees[ k ] = null;//合并完成之后,释放rhs内存 64 rhs.currentSize = 0; 65 }
重点介绍下二项队列合并为什么会有8种情况:
第25至27行,这8种情况可以用三个二进制位来表示:
//合并分8种情况 int whichCase = t1 == null ? 0 : 1; whichCase += t2 == null ? 0 : 2; whichCase += carry == null ? 0 : 4;
0<=whichCase<=7,一共8种情况。只分析一种情况,其他情况类似分析:
分析有rhs和this的情况。即,需要将 this 和 rhs 这两棵二项树合并,this代表当前二项树。二进制表示为 011
t1(this)不为空,whichCase=1,然后 t2为rhs,也不为空,故whichCase再加2。这里加2的原因是rhs是二进制中的第2位。
situation carry rhs this
no trees 0 0 0
only this 0 0 1
only rhs 0 1 0
only carry 1 0 0
this and rhs 0 1 1
.....
.....
All 1 1 1
carry表示上一步合并二项树过程上,生成的一棵新二项树。
确定了哪种合并情况后,再来看看对这些情况是如何处理的:
case 0: /* No trees */ case 1: /* Only this */ break;
第0种情况,表示没有树需要合并。第1种情况表示,只有this (当前二项树)树。什么叫只有当前二项树呢?(引用网友的一张图:)
黄色节点表示的是二项队列H(1),绿色节点表示的二项队列H(2),红色节点表示合并二项队列H(1)和H(2)之后,生成的新的二项队列H(3)。
H(2)中有一棵节点权值为13的高度为1的二项树,而H(1)中没有高度为1的二项树。此时就是rhs == null。即只有当前二项树(this树)
再来分析下case3情况:
case 3: /* this and rhs */ carry = combineTrees( t1, t2 ); theTrees[ i ] = rhs.theTrees[ i ] = null; break;
如上图,H(1)中有一棵根为12高度为1的二项树;H(2)中也有一棵高度为1,但根为14的二项树。此时this 和 rhs 都不为null。
调用combineTress(t1,t2)方法合并成一棵新的二项树,该二项树高度为2,用carray表示。这也是上面提到的” carry表示上一步合并二项树过程上,生成的一棵新二项树。“
生成carry之后,H(1)和H(2)中都已经没有高度为1的二项树了,因此执行: theTrees[ i ] = rhs.theTrees[ i ] = null;
再来分析下case7情况:
case 7: /* All three */ theTrees[ i ] = carry; carry = combineTrees( t1, t2 ); rhs.theTrees[ i ] = null; break;
还是参考上面图:H(1)、H(2)在执行了case3之后,这二个二项队列一共有三棵高度为2的二项树了。
第一棵是:case3中生成的。它的根结点的权值为14
第二棵是:H(1)中原来存在的。它的根结点的权值为12
第三棵是:H(2)中原来存在的。它的根结点的权值为23
因此,whichCase的值为7=1+2+4
代码中对该情况的处理是这样的(代码处理与图中画的有点不一样:图中画的是将两棵根的权值较小的二项树(第一棵和第二棵)合并而代码中合并的是第二棵和第三棵吧???。不过这不影响理解 ):
数组位置 i 处 保存上一步生成的高度为2的二项树。 theTrees[ i ] = carry;
合并原来存在的那两棵高度为2的二项树, carry = combineTrees( t1, t2 );
合并之后,释放rhs占用的空间, rhs.theTrees[ i ] = null;
至此,合并操作分析完毕,其他情况的合并类似于上面的分析。
②insert 操作
insert操作可以看作是特殊的合并操作。即rhs二项队列中只有一棵高度为0的二项树。插入操作的复杂度与是否存在高度为 i 的二项树有关,具体分析参考Mark Allen Weiss的书籍。平均情况下的时间复杂度为O(1)。
代码如下:
1 /** 2 * Insert into the priority queue, maintaining heap order. 3 * This implementation is not optimized for O(1) performance. 4 * @param x the item to insert. 5 */ 6 public void insert( AnyType x ) 7 { 8 merge( new BinomialQueue<>( x ) ); 9 }
③deleteMin操作
deleteMin操作的步骤如下:
1)寻找一棵具有最小权值的根的二项树,设为B(i)。
int minIndex = findMinIndex( );
AnyType minItem = theTrees[ minIndex ].element;
BinNode<AnyType> deletedTree = theTrees[ minIndex ].leftChild;
2)删除B(i)的根,得到若干棵二项树:B(0)、B(1)...B(i-1)。这些二项树组成一个新的二项队列 H‘‘
// Construct H‘‘ BinomialQueue<AnyType> deletedQueue = new BinomialQueue<>( ); deletedQueue.expandTheTrees( minIndex + 1 ); deletedQueue.currentSize = ( 1 << minIndex ) - 1; for( int j = minIndex - 1; j >= 0; j-- ) { deletedQueue.theTrees[ j ] = deletedTree; deletedTree = deletedTree.nextSibling; deletedQueue.theTrees[ j ].nextSibling = null; }
3)原来的二项队列,删除B(i)这棵根的权值最小的二项树后,得到的新的二项队列 H‘
// Construct H‘ theTrees[ minIndex ] = null; currentSize -= deletedQueue.currentSize + 1;
4)合并 H‘‘ 和 H‘ 即可
merge( deletedQueue );
整个deleteMin的实现代码如下:
/** * Remove the smallest item from the priority queue. * @return the smallest item, or throw UnderflowException if empty. */ public AnyType deleteMin( ) { if( isEmpty( ) ) throw new UnderflowException( ); int minIndex = findMinIndex( ); AnyType minItem = theTrees[ minIndex ].element; BinNode<AnyType> deletedTree = theTrees[ minIndex ].leftChild; // Construct H‘‘ BinomialQueue<AnyType> deletedQueue = new BinomialQueue<>( ); deletedQueue.expandTheTrees( minIndex + 1 ); deletedQueue.currentSize = ( 1 << minIndex ) - 1; for( int j = minIndex - 1; j >= 0; j-- ) { deletedQueue.theTrees[ j ] = deletedTree; deletedTree = deletedTree.nextSibling; deletedQueue.theTrees[ j ].nextSibling = null; } // Construct H‘ theTrees[ minIndex ] = null; currentSize -= deletedQueue.currentSize + 1; merge( deletedQueue ); return minItem; }
三,二项队列与二叉堆的比较
基本操作: insert(平均情况下) deleteMin merge
二项队列: O(1) O(logN) O(logN)
二叉堆: O(1) O(logN) O(N)
可见,二项队列有效地支持了merge操作。
但是,需要注意的是:二项队列的实现用到了链表,树中的每个元素存储在一个结点中,结点之间采用“左孩子右兄弟”表示法进行链接,此外还需要一个额外的数组来保存各棵二项树的根结点,存储开销要比二叉堆大。
而对于二叉堆的存储,则简单得多。它只需要一个一维数组即可存储各个元素。
四,参考资料
http://www.cnblogs.com/pacoson/p/5151886.html
《数据结构与算法分析 JAVA语言描述第三版》Mark Allen Weiss著
标签:
原文地址:http://www.cnblogs.com/hapjin/p/5468817.html