过度拟合（overfitting）

标签：

我们之前解决过一个理论问题：机器学习能不能起作用？现在来解决另一个理论问题：过度拟合。

正如之前我们看到的，很多时候我们必须进行nonlinear transform。但是我们又无法确定Q的值。Q过小，那么E_in会很大；Q过大，就会出现过度拟合问题。如下图所示：

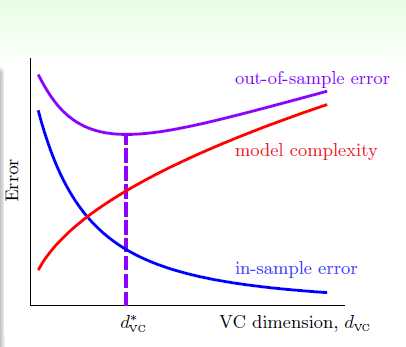
那么overfitting具体受什么因素影响呢？

现在我们又两个例子：

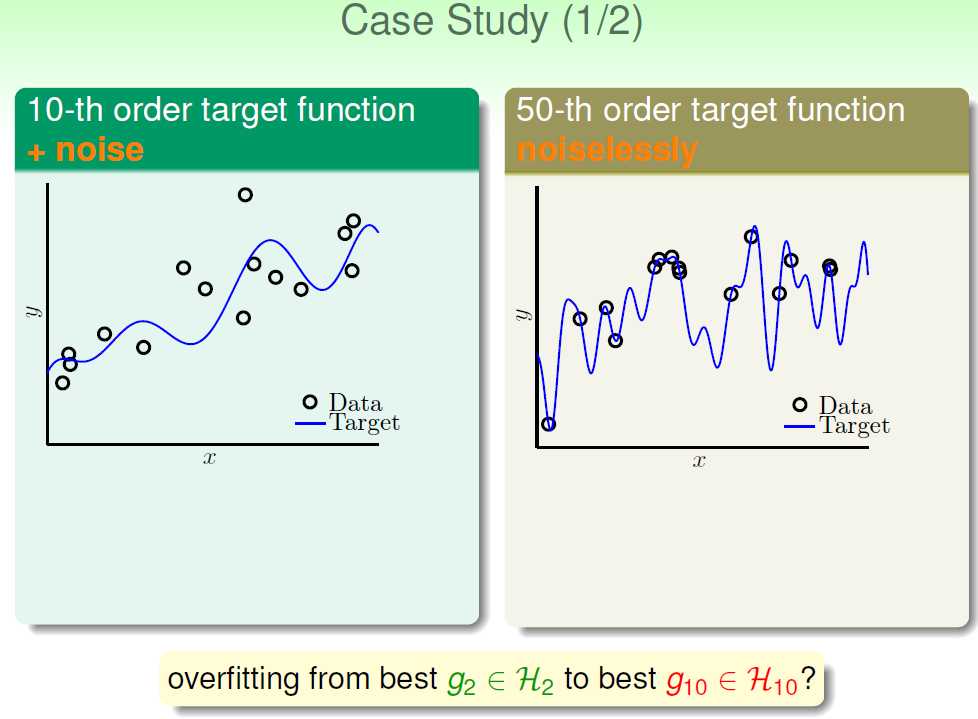
第一个例子的数据来源是：一个10-th的目标函数+noise；第二个例子的数据来源是：一个50-th的目标函数。现在我们用2-th函数（H₂）和10-th函数（H₁₀）分别对两个例子进行拟合。我们来预测一下结果。

我认为：对于这两个例子来说，H₁₀效果会更好。因为无论是对于第一个例子还是第二个例子，从阶数上来说，H₁₀都不存在overfitting问题。

下面是真正的结果：

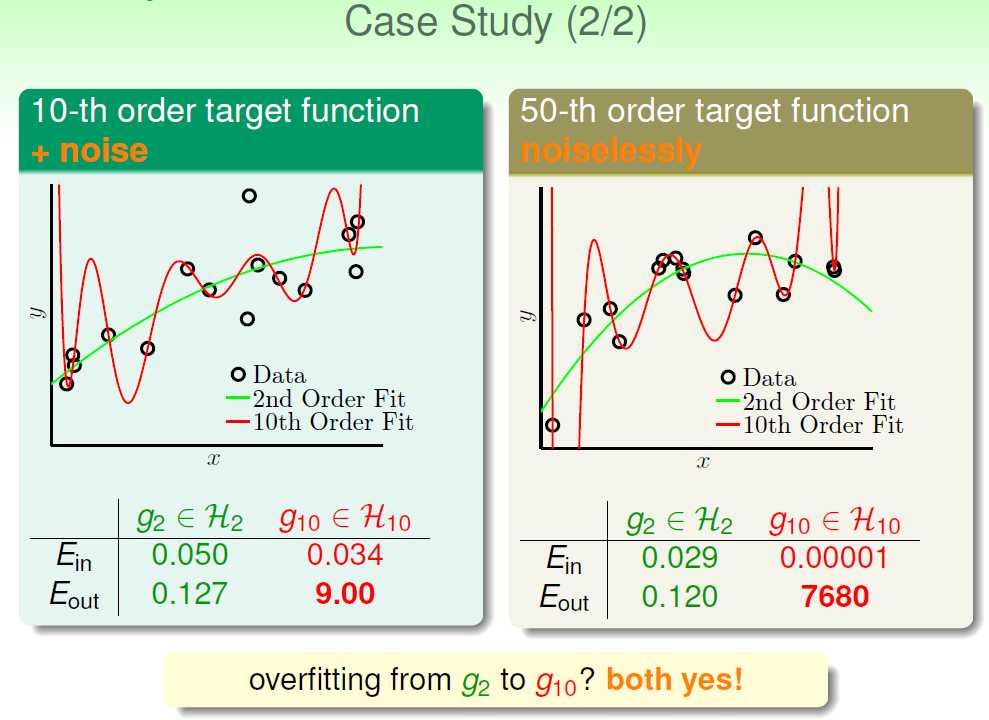
我们可以看出，对于两个例子，都是H₂效果最好。

通过这个违反直觉的例子，我们可以一窥overfitting的端倪。

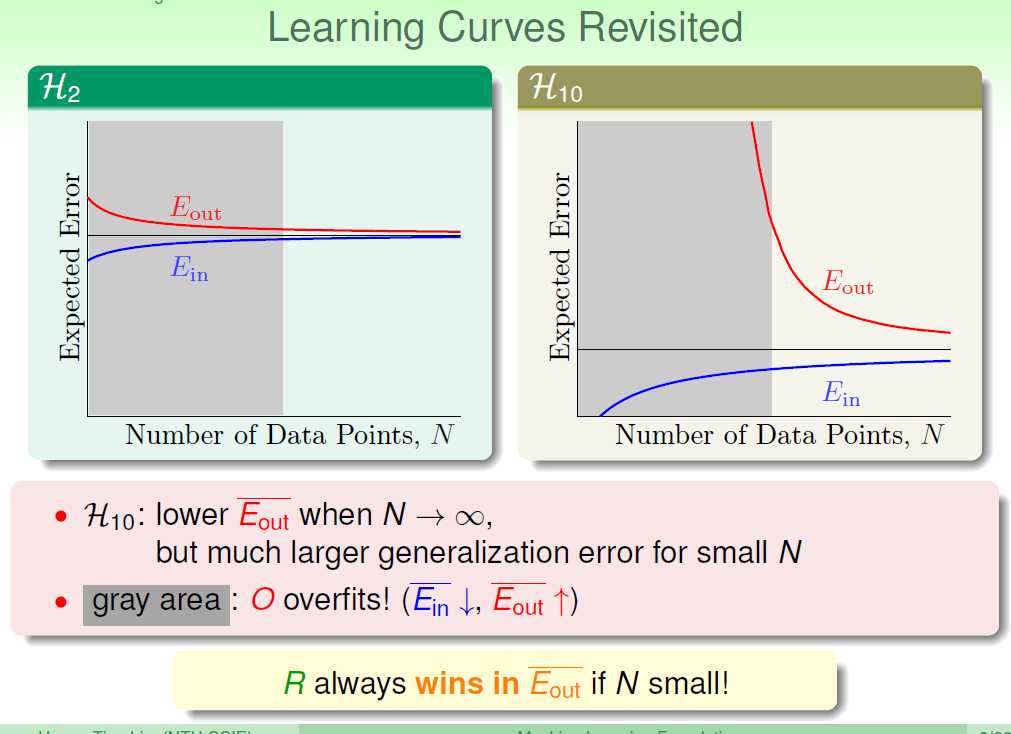
通过这个学习曲线，我们可以看出，H₁₀可以结果很好，但是是建立在N足够大的基础上；如果N很小的话，还是H₂的结果好！

补充一点：对于第二个例子，明明没有noise，为什么H₁₀表现的不如H₂呢？

因为50-th的复杂度太高，H₁₀和H₂都无法准确地拟合。此时目标函数的复杂度对于H₂和H₁₀来说，就相当于noise。

我们现在认为数据点数N、noise、还有目标函数的complexity level（阶数）Q都会影响overfitting。

下面进行详细说明。

从这个目标函数中，产生数据，然后用H2和H10去拟合。什么时候我们说会发生过度拟合呢？当使用H₁₀得到的E_out大于使用H₂得到的E_out，则必然发生了过度拟合，也即：overfit measure：E_out（g₁₀）-E_out（g₂）。

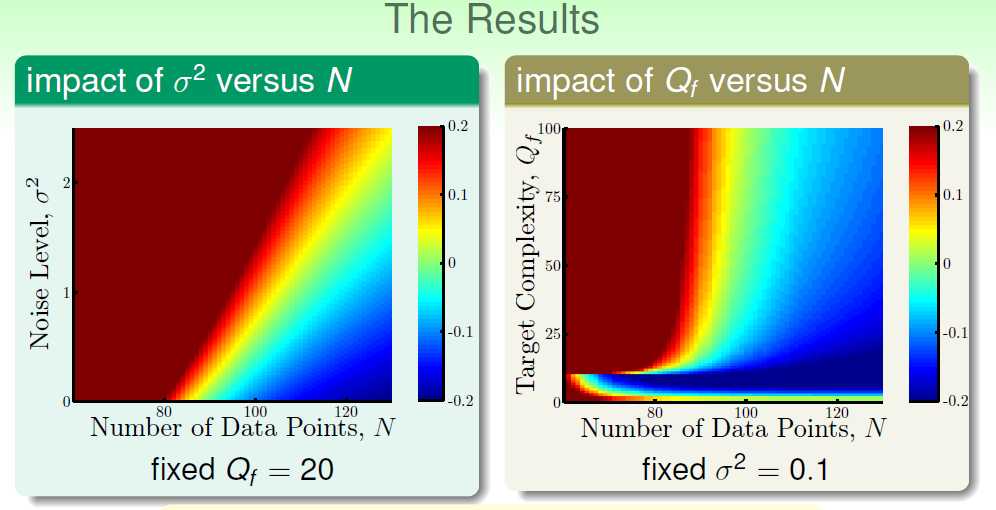
对于第一幅图，Q=20。我们可以很容易看到：1）N越小，noise越大，越容易发生过度拟合。2）当N很小的时候（此处为N<80），必然会发生过度拟合；3）当N很大，noise越大，越容易发生过度拟合。  N起到决定性作用。

对于第二幅图，noise固定。我们可以很容易看到：1）N约小，Q越大，越容易发生过度拟合；2）当N很小的时候，几乎必然会发生过度拟合；

第一幅图和第二幅图有所不同：1）对于左下方那一块红色区域，因为目标函数阶数足够小的时候，肯定会发生过度拟合。然而为什么随着N增加，反而不会有过度拟合了呢？2）当阶数够大，N很小的时候，就会发生过度拟合，但是一旦N足够大（此处N>100），就不会发生过度拟合了；

我们把noise成为stochastic noise，把Q成为deterministic noise。

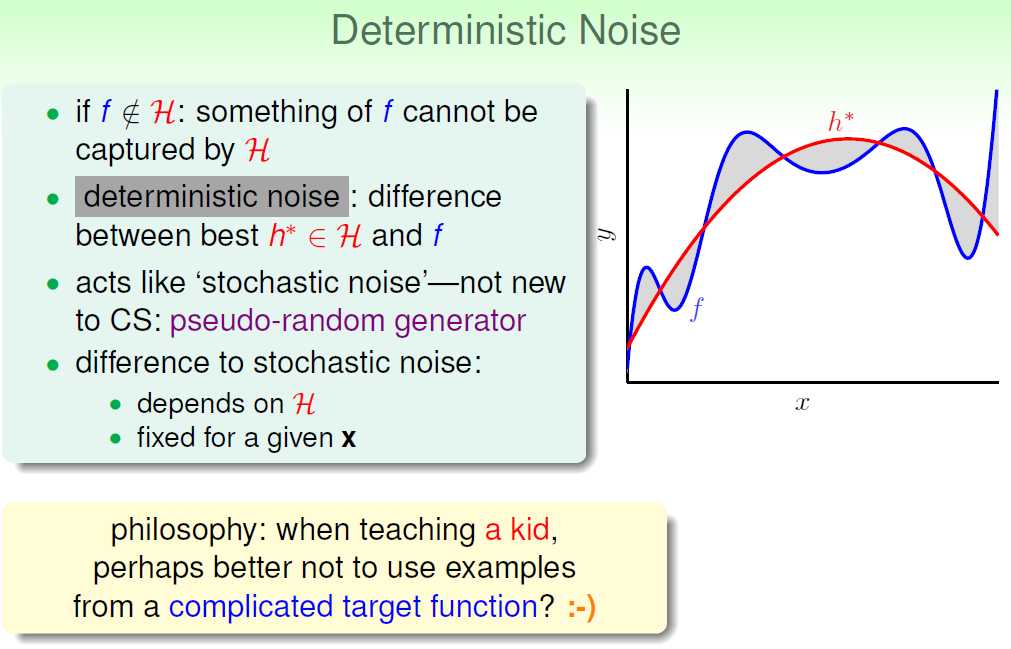
overfitting的几个影响因素，N（最重要），noise，Q。

如何解决overfitting问题呢？

我们把overfitting比作出了一起车祸，出车祸的原因可能是：开的太快了、路上有很多坑、路上的标识太少。与此对应的overfitting原因是：d_vc太大（Q太大）、noise太多、数据量太少。

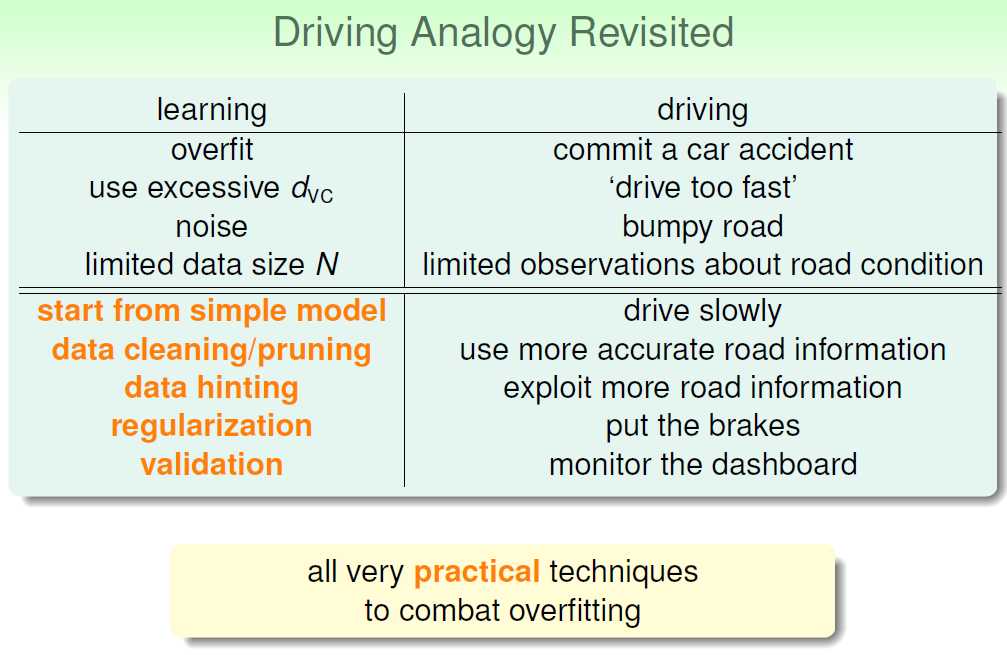
怎么避免“这起车祸”呢？可以开得慢一点，避开路面上的坑坑洼洼、或者是多获取一些路面标识。亦或者踩刹车、多看看仪表盘。

开的慢一点：从simple model开始；

避开路面坑坑洼洼：data cleaning：修正有noise的数据；data pruning：删除有noise的数据。

多获取路面标识：获取更多的数据（有可能无法实现）；或者采用Data Hinting技术；

踩刹车：regularization；

看仪表盘：validation。

后两个之后会详细讲述。

过度拟合（overfitting）

标签：

原文地址：http://www.cnblogs.com/wangyanphp/p/5469954.html