k近邻法（k-nearest neighbor, k-NN）

标签：

近邻法（-nearest neighbor, -NN）是一种基本的分类方法。

近邻法假设给定一个数据集，其中的样例类别已定。分类时，对新的样例，根据这个新样例的个最近邻的训练样例的类别，通过多数表决等方式进行预测。

因此，近邻法不具有显式的学习过程。值的选择、距离度量及分类决策规则是近邻法的三个基本要素。

近邻法于1968年由Cover和Hart提出。

给定训练集并且训练集，一共个样本，个维度，用表示数据集中的第个样本，用表示标记（类别）向量，代表第个样本的标记。

我们这时候要预测一个测试样例的标记，运用近邻法，按照以下步骤进行：

1. 根据选定的距离度量，在训练集中找出与最近邻的个样例，将这些样例表示为集合
2. 在中根据分类决策规则（如多数表决）决定的标记：

其中，为指示函数，即当时值为1，否则为0，为训练集的所有标记种类，为第个类别的标记。

当为1时，近邻法就被称为最近邻法。测试样例的类别就完成取决于离它最近的那个样例的类别。

下面我们谈谈近邻法的实现：树。

在实现近邻法的时候，最简单的实现方法肯定是线性扫描（linear scan），这时需要计算测试样例与训练集中的每一个训练实例的距离，当训练集很大时，计算非常耗时，这种方法是不可行的。

为了提高近邻搜索的效率，可以考虑使用特殊的结构存储训练数据，以减少计算距离的次数。具体的方法很多，在这里我们介绍树方法。

树是一种对维空间里中的实例点进行存储以便对其进行快速检索的树形数据结构。树是一个二叉树，表示对维空间的一个划分（partition）。构造树相当于不断地用垂直于坐标轴的超平面将维空间划分，构成一系列的维超矩形区域。树的每个结点都对应于一个维超矩形区域。

对于训练集，有个样例，维度为维，构造树的步骤如下：

1. 构造根结点，根结点对应于包含的所有样例的超矩形区域。
2. 选择第一维度为坐标轴，以中所有样例在第一维度上的值的中位数为切分点，将根结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与当前选定的坐标轴垂直的超平面实现。这样就由根结点生成了深度为1的左、右子结点：左子结点里面的所有样例在第一维度上的值小于切分点，右子结点里面的所有样例在第一维度上的值大于切分点。
3. 重复第2步，对于当前深度为的结点，选择第个维度为坐标轴，切分的过程与第2步相同。这样就由深度为的结点生成了深度为的左、右子结点。
4. 直到两个子区域没有实例存在时停止，从而形成树的区域划分。

举书上的例子，对于数据集，构造树，它的特征空间划分如下图所示：

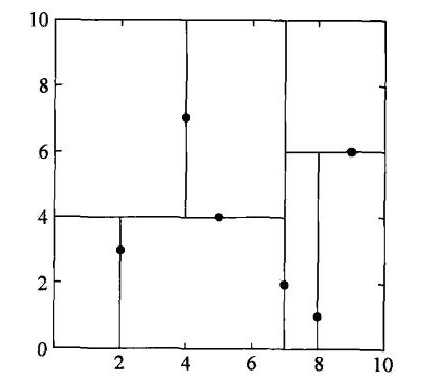
构造的树如下所示：

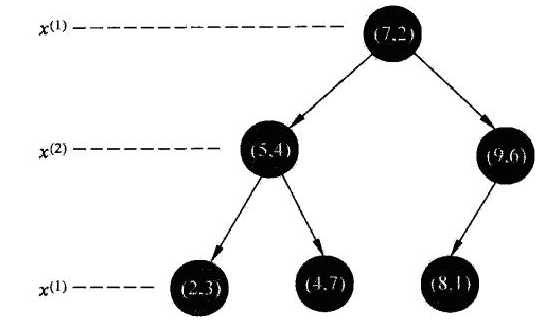
现在我们要利用树进行最近邻搜索，其图示如下：

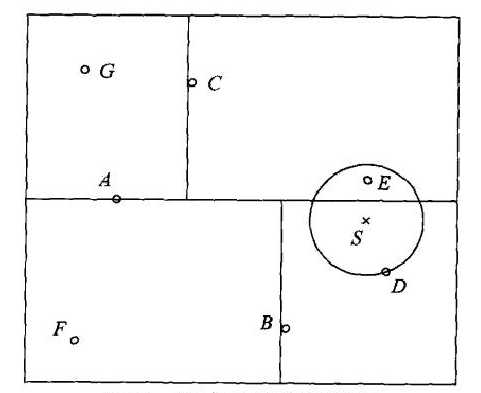
其中S为测试样例，用S首先找到了包含S的叶节点D，然后以画出S为圆心通过点D的圆，则最近邻一定在这个圆的内部。然后依次返回父结点，看是对应的区域是否与圆相交，比较其中的结点与当前最近点的距离，并进行更新，从而找出最近邻点。

k近邻法（k-nearest neighbor, k-NN）

标签：

原文地址：http://www.cnblogs.com/Rambler1995/p/5472262.html