堆（插入,删除）

标签：堆

首先呢，先来了解一个何为堆？

堆数据结构是一种数组对象，它可被视为一棵完全二叉树结构。

堆结构的二叉树存储是：

最大堆：每个父节点的都大于孩子节点

最小堆：每个父节点的都小于孩子节点

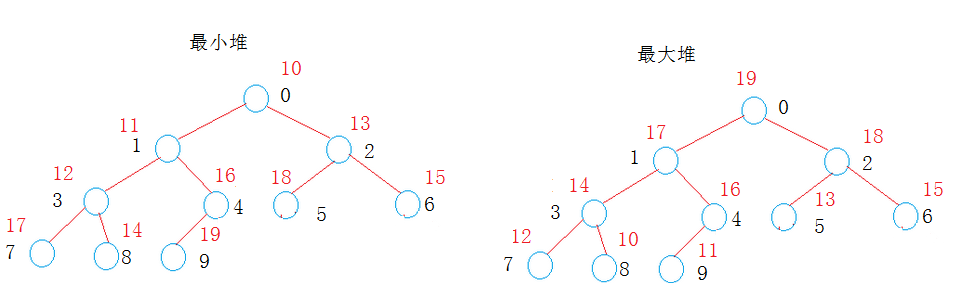最大堆：a[] = {19,17,18,14,16,13,15,12,10,11}

最小堆：a[] = {10,11,13,12,16,18,15,17,14,19}

代码实现最大堆：

#pragma once
#include <iostream>
#include <assert.h>
#include <vector>

using namespace std;

template <class T>
class Heap
{
public:
	Heap()   //无参构造函数
	{}

	Heap(T* a,size_t size)
	{
		for(size_t i=0;i<size;++i)
		{
			_a.push_back(a[i]);
		}
		//建堆
		for(int i=(_a.size()-2)/2;i>=0;--i)
		{
			_ApDown(i);
		}
	}

	void Push(const T& x)//插入元素
	{
		_a.push_back(x);//在堆尾插入元素
		_ApHeapUp(_a.size()-1);	//向上调整	
	}

	void Pop()//删除(删除优先级高)
	{
		swap(_a[0],_a[_a.size()-1]);//交换堆的第一个元素和最后一个元素
		_a.pop_back();//删除最后一个元素
		_ApDown(0);//向下调整
	}

	size_t Size()//堆的大小
	{
		return _a.size();
	}

	bool Empty()//堆是否为空
	{
		return _a.empty();
	}

public:
	void _ApDown(size_t parent) 
	{
		size_t child = parent*2+1;
		
		while(child < _a.size())
		{
			//找到左右孩子中较大的       
			if((child+1) < _a.size() && _a[child+1] > _a[child]) 
			{
				++child;
			}
			//比较较大孩子与父亲
			if(_a[child] > _a[parent]) //（2）
			{
				swap(_a[child],_a[parent]);
				parent = child;
				child = parent*2+1;
			}
			else
			{
				break;
			}
		}
	}

	void _ApHeapUp(size_t child)
	{
		size_t parent = (child-1)/2;
		while(child > 0)
		{
			if(_a[child] > _a[parent])//比较孩子与父亲 （3）
			{
				swap(_a[child],_a[parent]);
				child = parent;
				parent = (child-1)/2;
			}
			else
			{
				break;
			}
		}
	}
	
protected:
	vector<T> _a;
};

若要实现最小堆，可将上述代码中(1)(2)(3)处的大于改为小于即可。

但是这样使得代码冗余，不容易维护。

那么如何用一个来实现即可建最大堆也可建最小堆呢？我们之前见的仿函数就用上场喽！

回顾一下什么是仿函数？

仿函数的机制就是通过对（）进行重载。

template <class T>
struct Less  //小于
{
	bool operator()(const T& l,const T& r)
	{
		return l < r;
	}
};

template <class T>
struct Greater  //大于
{
	bool operator()(const T& l,const T& r)
	{
		return l > r;
	}
};

template <class T,class Comper = Greater<T> >//默认建大堆
class Heap
{
public:
	Heap()   //无参构造函数
	{}

	Heap(T* a,size_t size)
	{
		for(size_t i=0;i<size;++i)
		{
			_a.push_back(a[i]);
		}
		//建堆
		for(int i=(_a.size()-2)/2;i>=0;--i)
		{
			_ApDown(i);
		}
	}

	void Push(const T& x)//插入元素
	{
		_a.push_back(x);//在堆尾插入元素
		_ApHeapUp(_a.size()-1);	//向上调整	
	}

	void Pop()//删除(删除优先级高)
	{
		swap(_a[0],_a[_a.size()-1]);//交换堆的第一个元素和最后一个元素
		_a.pop_back();//删除最后一个元素
		_ApDown(0);//向下调整
	}

	size_t Size()//堆的大小
	{
		return _a.size();
	}

	bool Empty()//堆是否为空
	{
		return _a.empty();
	}

public:
	void _ApDown(size_t parent) 
	{
		size_t child = parent*2+1;
		
		while(child < _a.size())
		{
			Comper com;
			//找到左右孩子中较大的
			if((child+1) < _a.size() && com(_a[child+1],_a[child]))
			{
				++child;
			}
			//比较较大孩子与父亲
			if(com(_a[child],_a[parent]))
			{
				swap(_a[child],_a[parent]);
				parent = child;
				child = parent*2+1;
			}
			else
			{
				break;
			}
		}
	}

	void _ApHeapUp(size_t child)
	{
		size_t parent = (child-1)/2;
		Comper com;
		while(child > 0)
		{
			if(com(_a[child],_a[parent]))//比较孩子与父亲
			{
				swap(_a[child],_a[parent]);
				child = parent;
				parent = (child-1)/2;
			}
			else
			{
				break;
			}
		}
	}
	
protected:
	vector<T> _a;
};

测试函数：

void Test1()
{
	int a[] = {10,16,18,12,11,13,15,17,14,19};
	//Heap<int> hp(a,sizeof(a)/sizeof(a[0]));  //默认建大堆
	Heap<int,Less<int> > hp1(a,sizeof(a)/sizeof(a[0])); //建小堆
}

本文出自 “一起去看星星” 博客，转载请与作者联系！

堆（插入,删除）

标签：堆

原文地址：http://10810429.blog.51cto.com/10800429/1771303