deep learning 练习 牛顿法完成逻辑回归

标签：

                                             Logistic Regression and Newton‘s Method

作业链接：http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex4/ex4.html

数据是40个考上大学的小朋友和40个没有考上大学的小朋友在两次测验中的成绩，和他们是否通过的标签。

根据数据建立这两次测验与是否进入大学的二分类模型。

在二分类任务中，我们需要找到一个函数，来拟合特征输入X和预测输出Y，理想的函数是阶跃函数，但是由于阶跃函数不具备良好的数学性质（如可导性)，我们可以选择sigmoid函数。

牛顿法基本公式介绍

 使用S函数

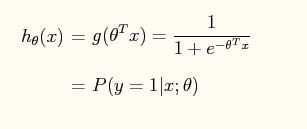
带入特征X之后，h(x)便可以看作是Y发生的概率，只是可以看作而已 。

损失函数J（）定义为：
          

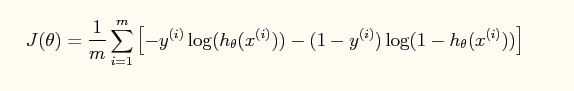
这个损失函数的定义是用的极大似然法，我们对对率回归模型最大化“对数似然”就可以得到，

极大似然本质就是让每个样本属于其真实标记的概率越大越好。

我们需要用牛顿法迭代参数来使损失函数达到最小值。

牛顿迭代公式如下

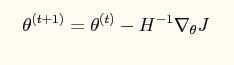
对应的梯度公式如下：

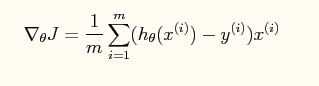
海森矩阵如下：

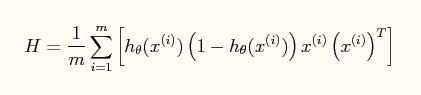
其中X(i)是n+1维的向量，X(i)*X(i)‘是(n+1)*(n+1)的矩阵，而h(x(i))和y(i)是归一化以后的数据。

这个公式在代码实现的时候，有一点点需要注意的，正确实现如下：

H=1./m.*(x‘*diag(h)*diag(1-h)‘*x);

其中diag(h)*diag(1-h)‘表示生成一个(n+1)*(n+1)矩阵，矩阵每一个对角元素是h*(1-h)。（我当时第一次敲公式的时候就直接敲成了h*(1-h)‘,结果死活迭代不对）

牛顿法对于迭代次数的要求不高，大约需要5-15次。但是牛顿法每次迭代的复杂度是O(n*3)，

与梯度下降法相比，梯度法对迭代次数要求很高，但是每次迭代的复杂度是O(n)。

所以在选择数值优化算法进行凸优化的时候，当n<1000时，我们优先选用牛顿法，当n>1000时，我们选择梯度下降。

代码实现：

clc 
clear all;
close all;
x = load(‘ex4x.dat‘);%加载数据
y = load(‘ex4y.dat‘);
%%%%--------------------数据预处理----------------------%%%%%%
m = length(y); 
x = [ones(m, 1), x];
% sigma = std(x);%取方差
% mu = mean(x);%取均值
% x(:,2) = (x(:,2) - mu(2))./ sigma(2);%归一化
% x(:,3) = (x(:,3) - mu(3))./ sigma(3);%归一化
g = inline(‘1.0 ./ (1.0 + exp(-z))‘); 
theta = zeros(size(x(1,:)))‘; % initialize fitting parameters

J = zeros(8, 1); %初始化损失函数
for num_iterations = 1:8
    h=g(x*theta);%计算S函数
    
    deltaJ=1/m.*x‘*(h-y);%梯度
    
    H = (1/m).*x‘ * diag(h) * diag(1-h) * x;
    
    J(num_iterations) = 1/m*sum(-y‘*log(h)-(1-y)‘*log(1-h));%牛顿法损失函数计算
    
    theta = theta-H^(-1)*deltaJ;%% 参数更新
end 
  x1=[1,20,80];
  h=g(x1*theta)%预测

   最后预测出来的概率是这个小朋友通过测试的概率，为0.332；

另外，牛顿法并不要求数据归一化，当然，你也可以这样做。

deep learning 练习 牛顿法完成逻辑回归

标签：

原文地址：http://www.cnblogs.com/YangQiaoblog/p/5475229.html