标签：

http://blog.csdn.net/pipisorry/article/details/51373090

马氏链收敛定理

马氏链定理： 如果一个非周期马氏链具有转移概率矩阵P,且它的任何两个状态是连通的，那么limn→∞Pnij 存在且与i无关，记limn→∞Pnij=π(j), 我们有

1. limn→∞Pn=???????π(1)π(1)?π(1)?π(2)π(2)?π(2)??????π(j)π(j)?π(j)?????????????

1.  π(j)=∑i=0∞π(i)Pij
2.  π 是方程 πP=π 的唯一非负解

其中,π=[π(1),π(2),?,π(j),?],∑i=0∞πi=1 π称为马氏链的平稳分布。

所有的 MCMC(Markov Chain Monte Carlo) 方法都是以这个定理作为理论基础的。 定理的证明相对复杂。

定理内容的一些解释说明

1. 该定理中马氏链的状态不要求有限，可以是有无穷多个的；
2. 定理中的“非周期“这个概念不解释，因为我们遇到的绝大多数马氏链都是非周期的；
3. 两个状态i,j是连通并非指i 可以直接一步转移到j(Pij>0),而是指i 可以通过有限的n步转移到达j(Pnij>0)。马氏链的任何两个状态是连通的含义是指存在一个n, 使得矩阵Pn 中的任何一个元素的数值都大于零。
4. 我们用 Xi 表示在马氏链上跳转第i步后所处的状态，如果limn→∞Pnij=π(j) 存在，很容易证明以上定理的第二个结论。由于
   
   P(Xn+1=j)=∑i=0∞P(Xn=i)P(Xn+1=j|Xn=i)=∑i=0∞P(Xn=i)Pij
   
   上式两边取极限就得到 π(j)=∑i=0∞π(i)Pij

皮皮blog

Metropolis-Hastings采样算法

马氏链的收敛定理非常重要，所有的 MCMC(Markov Chain Monte Carlo) 方法都是以这个定理作为理论基础的。

Idea

对于给定的概率分布p(x),我们希望能有便捷的方式生成它对应的样本。由于马氏链能收敛到平稳分布， 于是一个很的漂亮想法是：如果我们能构造一个转移矩阵为P的马氏链，使得该马氏链的平稳分布恰好是p(x), 那么我们从任何一个初始状态x0出发沿着马氏链转移, 得到一个转移序列 x0,x1,x2,?xn,xn+1?,， 如果马氏链在第n步已经收敛了，于是我们就得到了 π(x) 的样本xn,xn+1?。

这个绝妙的想法在1953年被 Metropolis想到了，为了研究粒子系统的平稳性质， Metropolis 考虑了物理学中常见的波尔兹曼分布的采样问题，首次提出了基于马氏链的蒙特卡罗方法，即Metropolis算法，并在最早的计算机上编程实现。Metropolis 算法是首个普适的采样方法，并启发了一系列 MCMC方法，所以人们把它视为随机模拟技术腾飞的起点。 Metropolis的这篇论文被收录在《统计学中的重大突破》中， Metropolis算法也被遴选为二十世纪的十个最重要的算法之一。

我们接下来介绍的MCMC 算法是 Metropolis 算法的一个改进变种，即常用的 Metropolis-Hastings 算法。由上一节的例子和定理我们看到了，马氏链的收敛性质主要由转移矩阵P 决定, 所以基于马氏链做采样的关键问题是如何构造转移矩阵P,使得平稳分布恰好是我们要的分布p(x)。如何能做到这一点呢？

细致平稳条件

定理：[细致平稳条件] 如果非周期马氏链的转移矩阵P和分布π(x) 满足

其实这个定理是显而易见的，因为细致平稳条件的物理含义就是对于任何两个状态i,j, 从 i 转移出去到j 而丢失的概率质量，恰好会被从 j 转移回i 的概率质量补充回来，所以状态i上的概率质量π(i)是稳定的，从而π(x)是马氏链的平稳分布。数学上的证明也很简单，由细致平稳条件可得

由于π 是方程 πP=π    的解，所以π是平稳分布。

Note: 细致平稳条件是达到稳态的充分条件，并不是必要条件。如在[马尔科夫模型]示例中0.28*0.286=0.08008，0.15*0.489=0.07335不相等，并不符合细致平稳条件。

构建满足条件的马氏链

假设我们已经有一个转移矩阵为Q马氏链(q(i,j)表示从状态i转移到状态j的概率，也可以写为q(j|i)或者q(i→j)), 显然，通常情况下

在改造 Q 的过程中引入的 α(i,j)称为接受率，物理意义可以理解为在原来的马氏链上，从状态i 以q(i,j) 的概率转跳转到状态j 的时候，我们以α(i,j)的概率接受这个转移，于是得到新的马氏链Q′的转移概率为q(i,j)α(i,j)。

Note：

1. 也就是说之前具有转移矩阵Q的马氏链可能收敛于另一个分布，所以我们要改造这个转移矩阵，使其转移矩阵Q’能够使新的马氏链收敛于p(x)。

2. 当按照上面介绍的构造方法把Q–>Q’后，就不能保证Q’是一个转移矩阵了，即Q’的每一行加和为1。这时应该在当 j != i 的时候概率Q‘(i, j) 就如上处理， 当j = i 的时候， Q‘(i, i) 应该设置Q‘(i, i) = 1- 其它概率之和，归一化概率转移矩阵。

马氏链转移和接受概率：

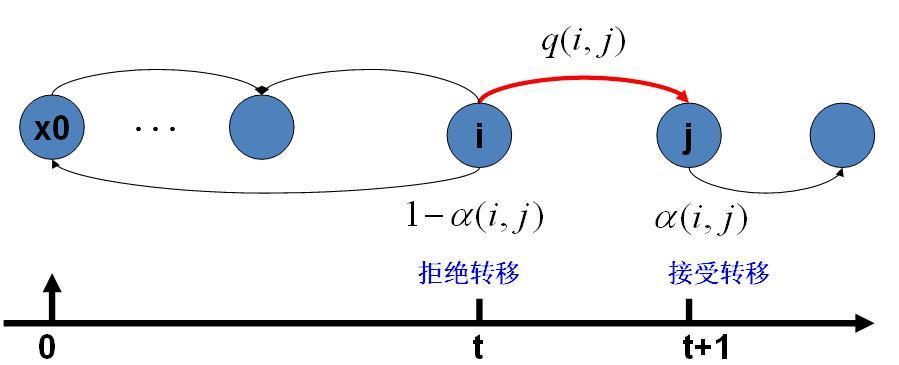
MCMC采样算法

采样概率分布p(x)的算法，假设我们已经有一个转移矩阵Q(对应元素为q(i,j))

Note: 一开始的采样还没有收敛，并不是平稳分布（p(x)）的样本，只有采样了多次（如20次）可能收敛了，其样本才算是平稳分布的样本。

Metropolis-Hastings算法

{提高接受率alpha}

上述过程中 p(x),q(x|y) 说的都是离散的情形，事实上即便这两个分布是连续的，以上算法仍然是有效，于是就得到更一般的连续概率分布 p(x)的采样算法，而q(x|y)   就是任意一个连续二元概率分布对应的条件分布。

以上的 MCMC 采样算法已经能很漂亮的工作了，不过它有一个小的问题：马氏链Q在转移的过程中的接受率α(i,j) 可能偏小，这样采样过程中马氏链容易原地踏步，拒绝大量的跳转，这使得马氏链遍历所有的状态空间要花费太长的时间，收敛到平稳分布p(x)的速度太慢。有没有办法提升一些接受率呢?

假设 α(i,j)=0.1,α(j,i)=0.2      , 此时满足细致平稳条件，于是

对于分布 p(x),我们构造转移矩阵Q′ 使其满足细致平稳条件

皮皮blog

Gibbs Sampling算法

吉布斯采样满足细致平稳条件的转移矩阵的构造

对于高维的情形，由于接受率 α的存在(通常α<1), 以上 Metropolis-Hastings 算法的效率不够高。能否找到一个转移矩阵Q使得接受率 α=1 呢？我们先看看二维的情形，假设有一个概率分布 p(x,y), 考察x坐标相同的两个点A(x1,y1),B(x1,y2)，我们发现

同样的，如果我们在 y=y1 这条直线上任意取两个点 A(x1,y1),C(x2,y1),也有如下等式

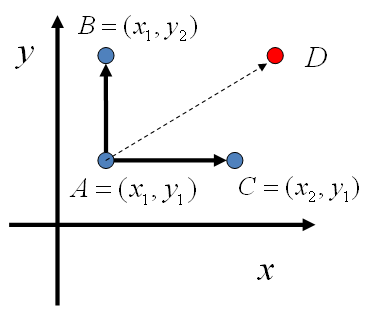
于是我们可以如下构造平面上任意两点之间的转移概率矩阵Q

有了如上的转移矩阵 Q, 我们很容易验证对平面上任意两点 X,Y, 满足细致平稳条件

二维吉布斯采样算法

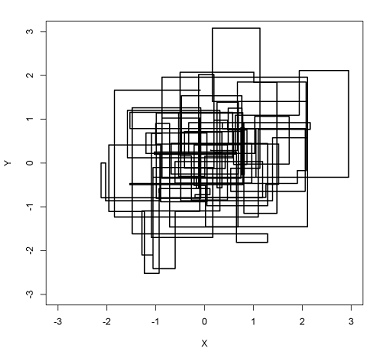
Gibbs Sampling 算法中的马氏链转移

    2.1步是从 (x0,y0)转移到(x0,y1)，满足Q(A→B)=p(yB|x1)的细致平稳条件，所以会收敛到平稳分布；同样2.2步是从(x0,y1)转移到(x1,y1)，也会收敛到平稳分布。也就是整个第2步是从 (x0,y0)转移到(x1,y1)，满足细致平稳条件，在循环多次后会收敛于平稳分布，采样得到的(xn,yn),(xn+1,yn+1)...就是平稳分布的样本（注意，并不是(xn,yn),(xn,yn+1),(xn+1,yn+1)...）。

    以上采样过程中，如图所示，马氏链的转移只是轮换的沿着坐标轴 x轴和y轴做转移，于是得到样本(x0,y0),(x0,y1),(x1,y1),(x1,y2),(x2,y2),? 马氏链收敛后，最终得到的样本就是 p(x,y) 的样本，而收敛之前的阶段称为 burn-in period。也就是说马氏链跳转过程中就是采样的过程， 马氏链任何一个时刻 i 到达的状态都 x_i 都是一个样本。 只是要等到 i 足够大( i > K) ， 马氏链收敛到平稳分布后, 那么 x_K, x_{K+1}, …. 这些样本就都是平稳分布的样本。lz提示一点，收敛到的平稳分布pi(x)是我们看不到的，我们看到的只是第t个循环的采样结果，在某个循环后，到达平稳分布pi(x)，在这之后的采样结果(xn,yn),(xn+1,yn+1)...统计一下计算不同样本的概率，就组成了我们可以看到的近似平稳分布（平稳分布的采样分布）。

坐标轴轮换采样

    一般地，Gibbs Sampling 算法大都是坐标轴轮换采样的，但是这其实是不强制要求的。最一般的情形可以是，在t时刻，可以在x轴和y 轴之间随机的选一个坐标轴，然后按条件概率做转移，马氏链也是一样收敛的。轮换两个坐标轴只是一种方便的形式。

n维吉布斯采样算法

以上的过程我们很容易推广到高维的情形，对于(***) 式，如果x1变为多维情形x1，可以看出推导过程不变，所以细致平稳条件同样是成立的

此时转移矩阵 Q 由条件分布 p(y|x1) 定义。上式只是说明了一根坐标轴的情形，和二维情形类似，很容易验证对所有坐标轴都有类似的结论。

所以n维空间中对于概率分布p(x1,x2,?,xn)  可以如下定义转移矩阵

1. 如果当前状态为(x1,x2,?,xn)，马氏链转移的过程中，只能沿着坐标轴做转移。沿着xi 这根坐标轴做转移的时候，转移概率由条件概率 p(xi|x1,?,xi?1,xi+1,?,xn) 定义；
2.  其它无法沿着单根坐标轴进行的跳转，转移概率都设置为 0。

于是我们可以把Gibbs Sampling 算法从采样二维的 p(x,y)   推广到采样n 维的 p(x1,x2,?,xn)

Note: Algorithm 8中的第2步的第6小步，x2(t)应为x2(t+1)。

以上算法收敛后，得到的(xn,yn),(xn+1,yn+1)...就是概率分布p(x1,x2,?,xn)的样本，当然这些样本并不独立，但是我们此处要求的是采样得到的样本符合给定的概率分布，并不要求独立。

同样的，在以上算法中，坐标轴轮换采样不是必须的，可以在坐标轴轮换中引入随机性，这时候转移矩阵 Q 中任何两个点的转移概率中就会包含坐标轴选择的概率，而在通常的 Gibbs Sampling 算法中，坐标轴轮换是一个确定性的过程，也就是在给定时刻t，在一根固定的坐标轴上转移的概率是1。

Note: ps:关于gibbs sampling的收敛，可以采用R^统计量。同时，可以多开几个chain进行模拟。判断收敛的时候，应该掐头去尾计算R^。在工程实践中我们更多的靠经验和对数据的观察来指定 Gibbs Sampling 中的 burn-in 的迭代需要多少次。当然可以一条链跑到黑，但是一条链跑到黑只能是写学术 paper 的做法， 在工程上还是要考虑很实际的速度和效率的问题，做 LDA 的时候我们就得考虑每秒钟能处理多少个请求,这时候不得不设置 burn-in。

from: http://blog.csdn.net/pipisorry/article/details/51373090

ref:随机采样方法整理与讲解（MCMC、Gibbs Sampling等）*

MCMC案例学习

Charles Geyer:为什么burn-in不是必要的Burn-In is Unnecessary

Charles Geyer:为什么一条链走到黑是正确的One Long Run in MCMC

LDA-math-MCMC 和 Gibbs Sampling*

PRML

其它蒙特卡罗方法silce sampling(连续采样M个点)

从随机过程到马尔科夫链蒙特卡洛方法

An Introduction to MCMC for Machine Learning，2003

Introduction to Monte Carlo Methods

随机采样和随机模拟：吉布斯采样Gibbs Sampling

标签：

原文地址：http://blog.csdn.net/pipisorry/article/details/51373090