Matlab学习 之 Multivariance Linear Regression

本文主要是来练习多变量线性回归问题（3个变量）。

那个时候用梯度下降法求解时，给出的学习率是固定的$0.7$。而本次实验中学习率需要自己来选择，因此我们应该从小到大（比如从$0.001$到$10$）来选择，通过观察损失值与迭代次数之间的函数曲线来决定使用哪个学习速率。

当有了学习速率$\alpha$后，则本问问题求解方法和上面的没差别。

本文要解决的问题是给出了$47$个训练样本，训练样本的$y$值为房子的价格，$x$属性有$2$个，一个是房子的大小，另一个是房子卧室的个数。需要通过这些训练数据来学习系统的函数，从而预测房子大小为$1650$，且卧室有$3$个的房子的价格。

实验基础：

dot(A,B):
表示的是向量A和向量B的内积。

系统的损失函数：

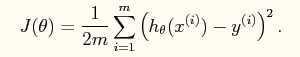
其向量表达形式如下：

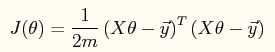
当使用梯度下降法进行参数的求解时，参数的更新公式如下：

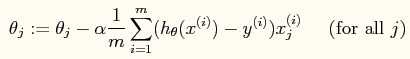
当然它也有自己的向量形式（程序中可以体现）。

实验结果：

测试学习率的结果如下：

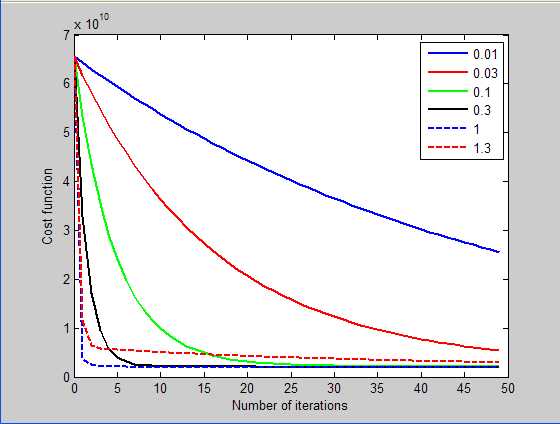
由此可知，选用学习率为1时，可以到达很快的收敛速度，因此最终的程序中使用的学习率为1.

最终使用梯度下降法和公式法的预测结果如下：

可以看出两者的结果是一致的。

实验主要程序及代码：

方法一：梯度下降法

x = load(‘ex3x.dat‘);
y = load(‘ex3y.dat‘);

x = [ones(size(x,1),1) x];
meanx = mean(x);%求均值
sigmax = std(x);%求标准偏差
x(:,2) = (x(:,2)-meanx(2))./sigmax(2);
x(:,3) = (x(:,3)-meanx(3))./sigmax(3);

figure
itera_num = 100; %尝试的迭代次数
sample_num = size(x,1); %训练样本的次数
alpha = [0.01, 0.03, 0.1, 0.3, 1, 1.3];%因为差不多是选取每个3倍的学习率来测试，所以直接枚举出来
plotstyle = {‘b‘, ‘r‘, ‘g‘, ‘k‘, ‘b--‘, ‘r--‘};

theta_grad_descent = zeros(size(x(1,:)));
for alpha_i = 1:length(alpha) %尝试看哪个学习速率最好
    theta = zeros(size(x,2),1); %theta的初始值赋值为0
    Jtheta = zeros(itera_num, 1);
    for i = 1:itera_num %计算出某个学习速率alpha下迭代itera_num次数后的参数       
        Jtheta(i) = (1/(2*sample_num)).*(x*theta-y)‘*(x*theta-y);%Jtheta是个行向量
        grad = (1/sample_num).*x‘*(x*theta-y);
        theta = theta - alpha(alpha_i).*grad;
    end
    plot(0:49, Jtheta(1:50),char(plotstyle(alpha_i)),‘LineWidth‘, 2)%此处一定要通过char函数来转换
    hold on

    if(1 == alpha(alpha_i)) %通过实验发现alpha为1时效果最好，则此时的迭代后的theta值为所求的值
        theta_grad_descent = theta
    end
end
legend(‘0.01‘,‘0.03‘,‘0.1‘,‘0.3‘,‘1‘,‘1.3‘);
xlabel(‘Number of iterations‘)
ylabel(‘Cost function‘)

%下面是预测公式
price_grad_descend = theta_grad_descent‘*[1 (1650-meanx(2))/sigmax(2) (3-meanx(3)/sigmax(3))]‘

方法二：normal equations

x = load(‘ex3x.dat‘);
y = load(‘ex3y.dat‘);
x = [ones(size(x,1),1) x];

theta_norequ = inv((x‘*x))*x‘*y
price_norequ = theta_norequ‘*[1 1650 3]‘