标签:
本文练习的是最简单的二元线性回归。
本题给出的是
比如legend(‘Training data’, ‘Linear regression’),它表示的是标出图像中各曲线标志所代表的意义,这里图像的第一条曲线(其实是离散的点)表示的是训练样本数据,第二条曲线(其实是一条直线)表示的是回归曲线。
hold on指在前一幅图的情况下打开画纸,允许在上面继续画曲线。hold off指关闭前一副画的画纸。
比如linspace(-3, 3, 100)指的是给出-3到3之间的100个数,均匀的选取,即线性的选取。
比如logspace(-2, 2, 15),指的是在10^(-2)到10^(2)之间选取15个数,这些数按照指数大小来选取,即指数部分是均匀选取的,但是由于都取了10为底的指数,所以最终是服从指数分布选取的。
采用normal equations方法求解:
x = load(‘ex2x.dat‘);
y = load(‘ex2y.dat‘);
plot(x,y,‘*‘)
xlabel(‘height‘)
ylabel(‘age‘)
sz = size(x)
x = [ones(sz),x];
w = inv(x‘*x)*x‘*y
hold on
%plot(x,0.0639*x+0.7502)
plot(x(:,2),0.0639*x(:,2)+0.7502)%更正后的代码采用gradient descend过程求解:
% Exercise 2 Linear Regression
% Data is roughly based on 2000 CDC growth figures
% for boys
%
% x refers to a boy‘s age
% y is a boy‘s height in meters
%
clear all; close all; clc
x = load(‘ex2x.dat‘); y = load(‘ex2y.dat‘);
m = length(y); % number of training examples
% Plot the training data
figure; % open a new figure window
plot(x, y, ‘o‘);
ylabel(‘Height in meters‘)
xlabel(‘Age in years‘)
% Gradient descent
x = [ones(m, 1) x]; % Add a column of ones to x
theta = zeros(size(x(1,:)))‘; % initialize fitting parameters
MAX_ITR = 1500;
alpha = 0.07;
for num_iterations = 1:MAX_ITR
% This is a vectorized version of the
% gradient descent update formula
% It‘s also fine to use the summation formula from the videos
% Here is the gradient
grad = (1/m).* x‘ * ((x * theta) - y);
% Here is the actual update
theta = theta - alpha .* grad;
% Sequential update: The wrong way to do gradient descent
% grad1 = (1/m).* x(:,1)‘ * ((x * theta) - y);
% theta(1) = theta(1) + alpha*grad1;
% grad2 = (1/m).* x(:,2)‘ * ((x * theta) - y);
% theta(2) = theta(2) + alpha*grad2;
end
% print theta to screen
theta
% Plot the linear fit
hold on; % keep previous plot visible
plot(x(:,2), x*theta, ‘-‘)
legend(‘Training data‘, ‘Linear regression‘)%标出图像中各曲线标志所代表的意义
hold off % don‘t overlay any more plots on this figure,指关掉前面的那幅图
% Closed form solution for reference
% You will learn about this method in future videos
exact_theta = (x‘ * x)\x‘ * y
% Predict values for age 3.5 and 7
predict1 = [1, 3.5] *theta
predict2 = [1, 7] * theta
% Calculate J matrix
% Grid over which we will calculate J
theta0_vals = linspace(-3, 3, 100);
theta1_vals = linspace(-1, 1, 100);
% initialize J_vals to a matrix of 0‘s
J_vals = zeros(length(theta0_vals), length(theta1_vals));
for i = 1:length(theta0_vals)
for j = 1:length(theta1_vals)
t = [theta0_vals(i); theta1_vals(j)];
J_vals(i,j) = (0.5/m) .* (x * t - y)‘ * (x * t - y);
end
end
% Because of the way meshgrids work in the surf command, we need to
% transpose J_vals before calling surf, or else the axes will be flipped
J_vals = J_vals‘;
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel(‘\theta_0‘); ylabel(‘\theta_1‘);
% Contour plot
figure;
% Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 2, 15))%画出等高线
xlabel(‘\theta_0‘); ylabel(‘\theta_1‘);%类似于转义字符,但是最多只能是到参数0~9训练样本散点和回归曲线预测图:
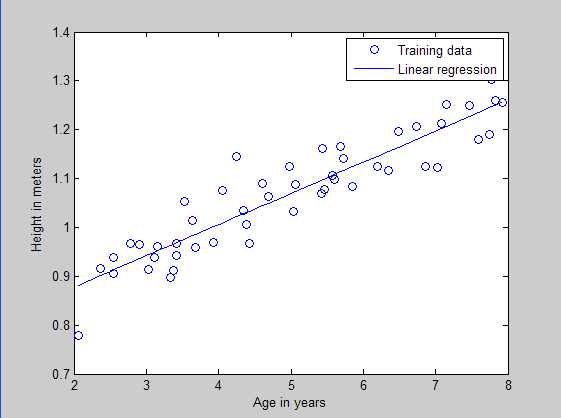
损失函数与参数之间的曲面图:
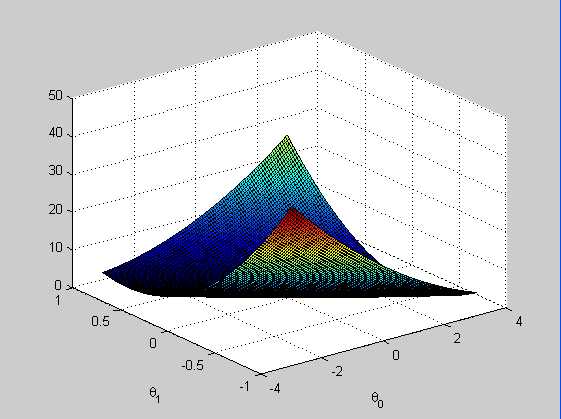
损失函数的等高线图:
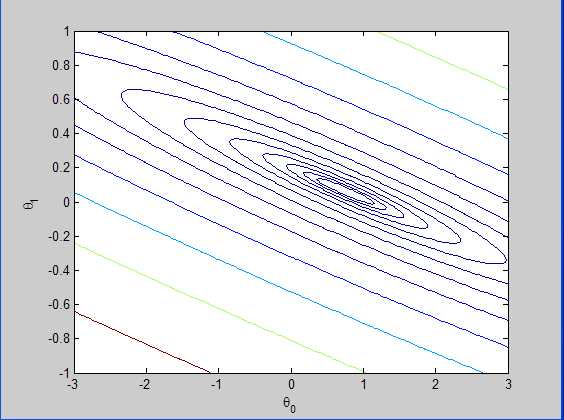
标签:
原文地址:http://blog.csdn.net/u013007900/article/details/51344770