标签:
1大搬家
Problem Description
近期B厂组织了一次大搬家,所有人都要按照指示换到指定的座位上。指示的内容是坐在位置i上的人要搬到位置j上。现在B厂有N个人,一对一到N个位置上。搬家之后也是一一对应的,改变的只有位次。
在第一次搬家后,度度熊由于疏忽,又要求大家按照原指示进行了一次搬家。于是,机智的它想到:再按这个指示搬一次家不就可以恢复第一次搬家的样子了。于是,B厂史无前例的进行了连续三次搬家。
虽然我们都知道度度熊的“机智”常常令人堪忧,但是不可思议的是,这回真的应验了。第三次搬家后的结果和第一次的结果完全相同。
那么,有多少种指示会让这种事情发生呢?如果两种指示中至少有一个人的目标位置不同,就认为这两种指示是不相同的。
Input
第一行一个整数TTT,表示T组数据。 每组数据包含一个整数N(1≤N≤1000000)。
Output
对于每组数据,先输出一行 Case #i: 然后输出结果,对1000000007取模。
Sample Input
2 1 3
Sample Output
Case #1: 1 Case #2: 4
//第三次搬家后的结果和第一次的结果完全相同,这表明搬家的指令必定符合如下规则:i-->t--->i
//由于直接推导f(N)(N个位置下指示个数)显得困难,于是很自然地考虑f(N+1)和f(N)是否存在递推关系,我们作图如下:
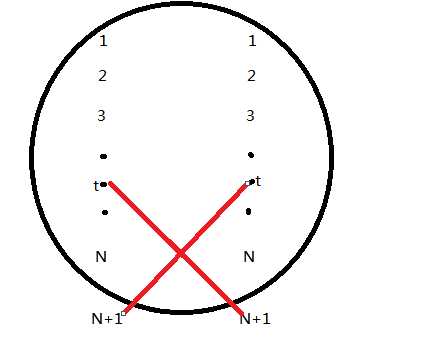
容易得到递推式f[N+1]=f(N)+N*f(N-1)
同时f(0)=f(1)=1(因f(2)=f(1)+f(0)=2)
#include <stdio.h> #define ll long long #define MAXN 1000001 #define mod 1000000007 int F[MAXN]; int main() { int T,N,i; scanf("%d",&T); F[1] = F[0] = 1; for(i=2;i<=MAXN;i++) { F[i] = F[i-1]%mod + (i-1)*(ll)F[i-2]%mod; F[i] %= mod; } // F[i] = F[i-1]%mod + (i-1)*(ll)F[i-2]%mod; //上面这样写,导致F[MAXN-1],F[MAXN-2]...可能大于mod // F[MAXN] %= mod; for(i=1;i<=T;i++) { scanf("%d",&N); printf("Case #%d:\n%d\n",i,F[N]); } return 0; }
2.列变位法解密
Problem Description
列变位法是古典密码算法中变位加密的一种方法,具体过程如下 将明文字符分割成个数固定的分组(如5个一组,5即为密钥),按一组一行的次序整齐排列,最后不足一组不放置任何字符,完成后按列读取即成密文。 比如: 原文:123456789 密钥:4 变换后的矩阵: 1234 5678 9xxx (最后的几个x表示无任何字符,不是空格,不是制表符,就没有任何字符,下同) 密文:159263748 再比如: 原文:Hello, welcome to my dream world! 密钥:7 变换后的矩阵: Hello, welcome to my dream w orld!xx 密文: Hw doeetrrlloellc adoomm!,my e w 实现一个利用列变位法的加密器对Bob来说轻而易举,可是,对Bob来说,想清楚如何写一个相应的解密器似乎有点困难,你能帮帮他吗?
Input
第一行一个整数TTT,表示TTT组数据。 每组数据包含222行 第一行,一个字符串s(1≤∣s∣≤1e5)),表示经过列变位法加密后的密文 第二行,一个整数K(1≤K≤∣s∣)),表示原文在使用列变位法加密时的密钥 输入保证密文字符串中只含有ASCII码在[0x20,0x7F)范围内的字符
Output
对于每组数据,先输出一行
Case #i:
然后输出一行,包含一个字符串s_decrypt,表示解密后得到的明文
Sample Input
4 159263748 4 Hw doeetrrlloellc adoomm!,my e w 7 Toodming is best 16 sokaisan 1
Sample Output
Case #1: 123456789 Case #2: Hello, welcome to my dream world! Case #3: Toodming is best Case #4: sokaisan
//原文通过转换矩阵得到密文,我们要通过密文得到原文,必须要借助转换矩阵的性质(但不能直接转换成矩阵后再输出--超时)
//找到对应字符后即实现输出,以第一行为例,第一个字符即为密文的首字符(实际上,密文的前 l=strlen(s)/K+(strlen(s)%K!=0)个字符即对应着转换矩阵的第一列)
//输出第二个字符及后面的字符时,必须考虑最后一行对应列是否为‘x‘(即不存在),若存在,则下一列在密文中的位置为前一列+len(即strlen(s)/K)+(mod!=0),否则+len
//依此输出前len行,然后判断mod(即strlen(s)%K)是否为0,不为0,代表最后一行有mod个元素要输出,j*(len+1)-1即为对应列在密文中的位置
#include <stdio.h> #include <string.h> #define clen 10001 char s[clen]; int main() { int T,K,i,k,j,len,mod,d; scanf("%d",&T); for(i=1;i<=T;i++) { getchar(); gets(s); scanf("%d",&K); printf("Case #%d:\n",i); len = (int)strlen(s)/K; mod = (int)strlen(s)%K; //decode for(k=0;k<len;k++) { for(j=0;j<=mod;j++) printf("%c",s[k+j*(len+(mod!=0))]); d = k+mod*(len+(mod!=0)); for(;j<K;j++) printf("%c",s[d+(j-mod)*len]);//间距要发生变化 } if(mod)// output the last list { for(j=1;j<=mod;j++) printf("%c",s[j*(len+1)-1]); } printf("\n"); } return 0; }
4.放盘子
Problem Description
小度熊喜欢恶作剧。今天他向来访者们提出一个恶俗的游戏。他和来访者们轮流往一个正多边形内放盘子。最后放盘子的是获胜者,会赢得失败者的一个吻。玩了两次以后,小度熊发现来访者们都知道游戏的必胜策略。现在小度熊永远是先手,他想知道他是否能获胜。
注意盘子不能相交也不能和多边形相交也不能放在多边形外。就是说,盘子内的点不能在多边形外或者别的盘子内。
Input
第一行一个整数T,表示T组数据。每组数据包含3个数n,a,r(4≤n≤100,0<a<1000,0<r<1000) n是偶数,代表多边形的边数,a代表正多边形的边长,r代表盘子的半径。
Output
对于每组数据,先输出一行
Case #i:
然后输出结果.如果小度熊获胜,输出”Give me a kiss!” 否则输出”I want to kiss you!”
Sample Input
2 4 50 2.5 4 5.5 3
Sample Output
Case #1: Give me a kiss! Case #2: I want to kiss you!
//由于多边形的边数n为偶数,很自然地用到对称性,即先下的度度熊先尝试在正多边形放圆盘,若不能放,则显然圆盘无法放入正多边形
//度度熊输,否则只要度度熊对称(以中心)地放,无论什么时候不能放盘,度度熊都赢,则实际上只要比较圆盘半径和正多边形中心到边的距离即可
#include <stdio.h> #include <math.h> #define pi 3.14159265 int main() { int T,n,i; double a,r; scanf("%d",&T); for(i=1;i<=T;i++) { scanf("%d%lf%lf",&n,&a,&r); printf("Case #%d:\n",i); if( a/(2*tan(pi/n)) >= r) puts("Give me a kiss!"); else puts("I want to kiss you!"); } return 0; }
标签:
原文地址:http://www.cnblogs.com/520xiuge/p/5492162.html