标签:
今天完成了机器人视觉的所有课程以及作业,确实是受益匪浅啊!

最后一个话题是Bundle Adjustment. 机器人视觉学中,最顶尖的方法。
1、基于非线性优化的相机位姿估计
之前已经在拟合一篇中,已经补完了非线性最小二乘拟合问题。Bundle Adjustment,中文是光束平差法,就是利用非线性最小二乘法来求取相机位姿,三维点坐标。在仅给定相机内部矩阵的条件下,对四周物体进行高精度重建。Bundle Adjustment的优化目标依旧是最小重复投影误差。
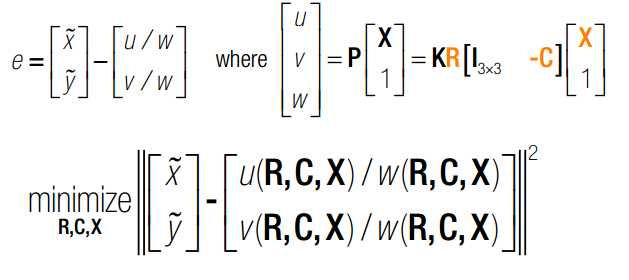
与利用non-linear mean square 解三角同,bundle adjustment 中所有的参数,RCX均为变量。N幅图则有N个位姿,X个点,我们会得到非常大的jacobbian Matrix.本质上,需要使用雅克比矩阵进行梯度下降搜索。详细见博客——拟合
2、雅克比矩阵
雅克比矩阵的行代表信息,列代表约束
每一行是一个点在该位姿下的误差,每一列代表f对x分量的偏导数。
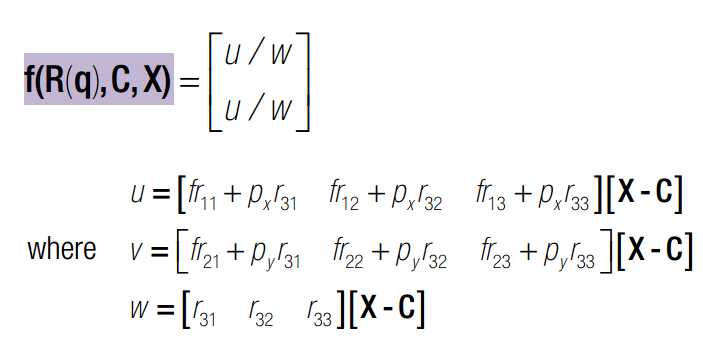
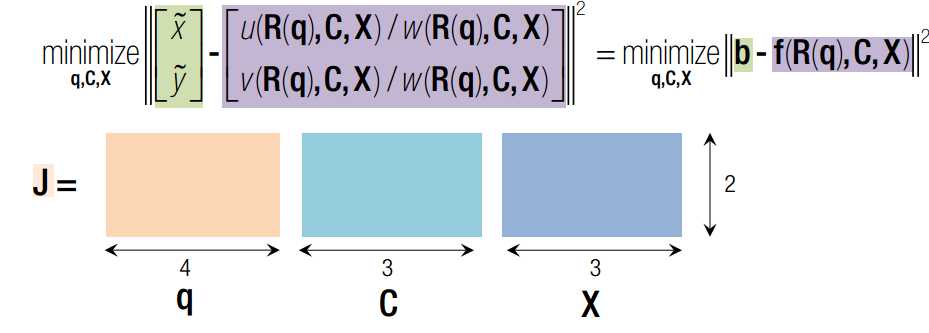
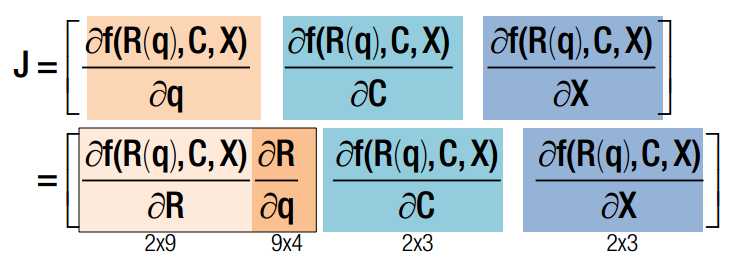
q x c 均为变量,q是旋转四元素,x 是三维点空间坐标,c 是相机光心在世界坐标系下的坐标。J 可以分为三部分,前4列代表对旋转求导,中间三列代表对c求导,最后三列代表对x求导。其中,对旋转求导又可以分解为对旋转矩阵求导X旋转矩阵对四元素q求导。一旦获得J的表达式,我们就可以使用Newton-Gaussian 迭代对x寻优了。求导后的数学表达式如下:
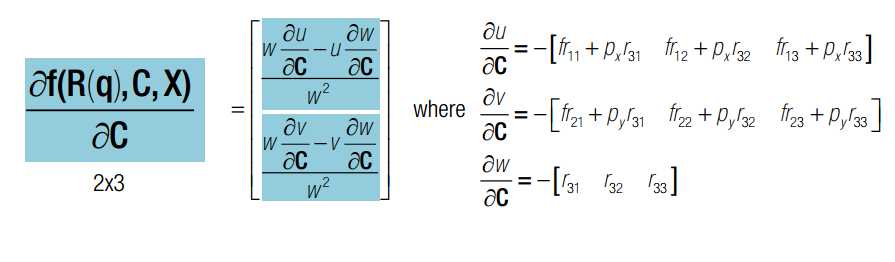
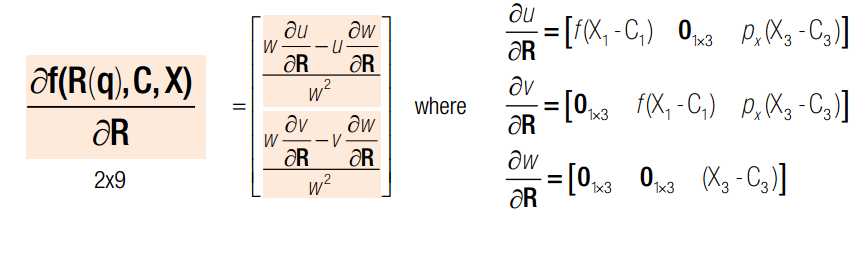
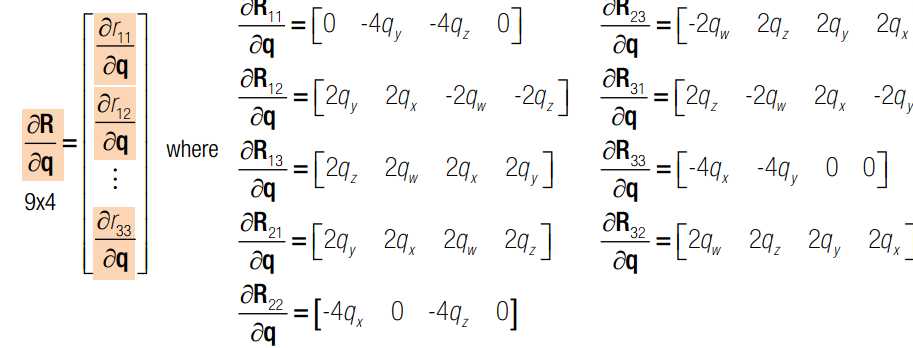
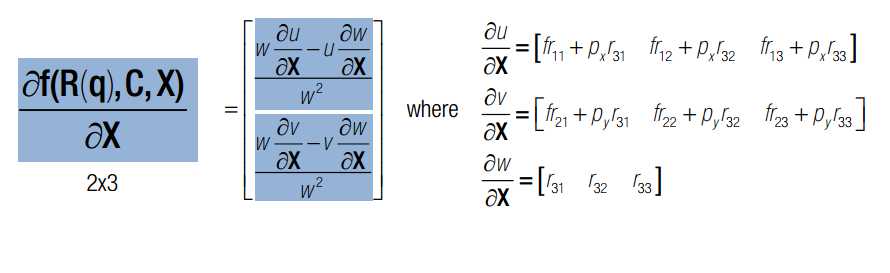
如果有两个相机,则总的雅克比矩阵如下:
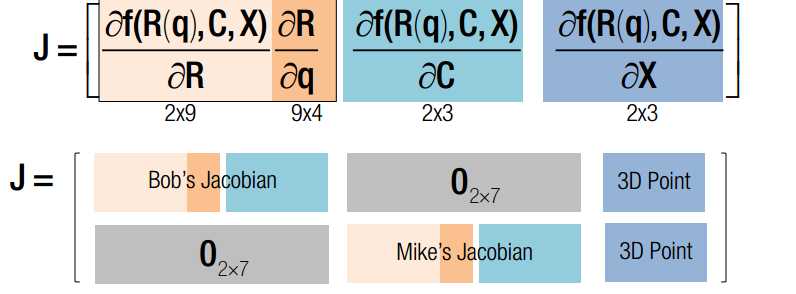
通过同时迭代所有的q C X ,最终可以同时得到世界点坐标,相机位姿 == SLAM!!!
机器人学 —— 机器人视觉(Bundle Adjustment)
标签:
原文地址:http://www.cnblogs.com/ironstark/p/5493030.html