标签：
广度优先搜索（也称宽度优先搜索，缩写BFS，以下采用广度来描述）是连通图的一种遍历策略。因为它的思想是从一个顶点V0开始，辐射状地优先遍历其周围较广的区域，故得名。
一般可以用它做什么呢？一个
算法导论里边会给出不少严格的证明，我想尽量写得通俗一点，因此采用一些直观的讲法来伪装成证明，关键的point能够帮你get到就好。
刚刚说的广度优先搜索是连通图的一种遍历策略，那就有必要将图先简单解释一下。
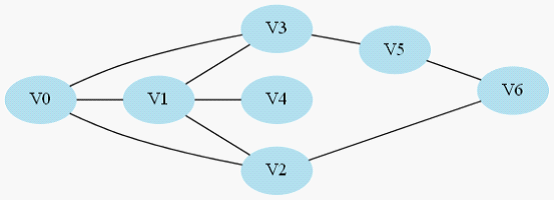
图2-1 连通图示例图
如图2-1所示，这就是我们所说的连通图，这里展示的是一个无向图，连通即每2个点都有至少一条路径相连，例如V0到V4的路径就是V0->V1->V4。
一般我们把顶点用V缩写，把边用E缩写。
常常我们有这样一个问题，从一个起点开始要到一个终点，我们要找寻一条最短的路径，从图2-1举例，如果我们要求V0到V6的一条最短路（假设走一个节点按一步来算）【注意：此处你可以选择不看这段文字直接看图3-1】，我们明显看出这条路径就是V0->V2->V6，而不是V0->V3->V5->V6。先想想你自己刚刚是怎么找到这条路径的：首先看跟V0直接连接的节点V1、V2、V3，发现没有V6，进而再看刚刚V1、V2、V3的直接连接节点分别是：{V0、V4}、{V0、V1、V6}、{V0、V1、V5}（这里画删除线的意思是那些顶点在我们刚刚的搜索过程中已经找过了，我们不需要重新回头再看他们了）。这时候我们从V2的连通节点集中找到了V6，那说明我们找到了这条V0到V6的最短路径：V0->V2->V6，虽然你再进一步搜索V5的连接节点集合后会找到另一条路径V0->V3->V5->V6，但显然他不是最短路径。
你会看到这里有点像辐射形状的搜索方式，从一个节点，向其旁边节点传递病毒，就这样一层一层的传递辐射下去，知道目标节点被辐射中了，此时就已经找到了从起点到终点的路径。
我们采用示例图来说明这个过程，在搜索的过程中，初始所有节点是白色（代表了所有点都还没开始搜索），把起点V0标志成灰色（表示即将辐射V0），下一步搜索的时候，我们把所有的灰色节点访问一次，然后将其变成黑色（表示已经被辐射过了），进而再将他们所能到达的节点标志成灰色（因为那些节点是下一步搜索的目标点了），但是这里有个判断，就像刚刚的例子，当访问到V1节点的时候，它的下一个节点应该是V0和V4，但是V0已经在前面被染成黑色了，所以不会将它染灰色。这样持续下去，直到目标节点V6被染灰色，说明了下一步就到终点了，没必要再搜索（染色）其他节点了，此时可以结束搜索了，整个搜索就结束了。然后根据搜索过程，反过来把最短路径找出来，图3-1中把最终路径上的节点标志成绿色。
整个过程的实例图如图3-1所示。
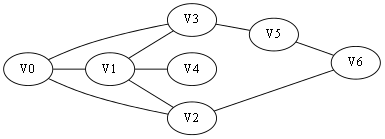初始全部都是白色（未访问）
即将搜索起点V0（灰色）
已搜索V0，即将搜索V1、V2、V3
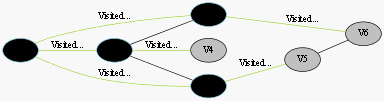……终点V6被染灰色，终止
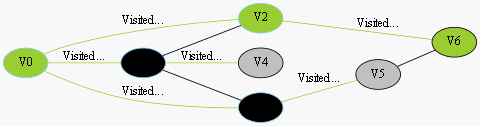找到最短路径
图3-1 寻找V0到V6的过程
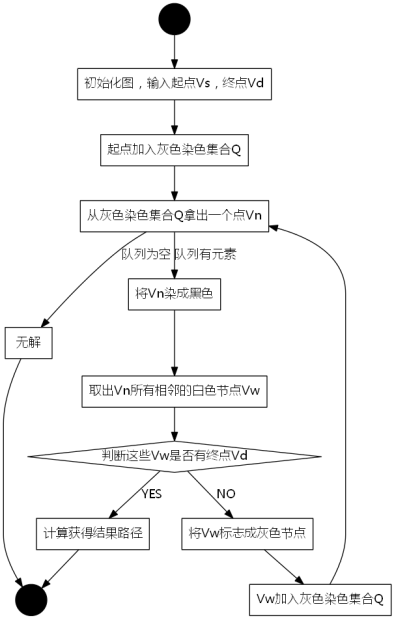
图3-2 广度优先搜索的流程图
在写具体代码之前有必要先举个实例，详见第4节。
第一节就讲过广度优先搜索适用于迷宫类问题，这里先给出POJ3984《迷宫问题》。
《迷宫问题》
定义一个二维数组：
int maze[5][5] = {
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
};
它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。
题目保证了输入是一定有解的。
也许你会问，这个跟广度优先搜索的图怎么对应起来？BFS的第一步就是要识别图的节点跟边！
节点就是某种状态，边就是节点与节点间的某种规则。
对应于《迷宫问题》，你可以这么认为，节点就是迷宫路上的每一个格子（非墙），走迷宫的时候，格子间的关系是什么呢？按照题目意思，我们只能横竖走，因此我们可以这样看，格子与它横竖方向上的格子是有连通关系的，只要这个格子跟另一个格子是连通的，那么两个格子节点间就有一条边。
如果说本题再修改成斜方向也可以走的话，那么就是格子跟周围8个格子都可以连通，于是一个节点就会有8条边（除了边界的节点）。
对应于题目的输入数组：
0, 1, 0, 0, 0,
0, 1, 0, 1, 0,
0, 0, 0, 0, 0,
0, 1, 1, 1, 0,
0, 0, 0, 1, 0,
我们把节点定义为(x,y)，(x,y)表示数组maze的项maze[x][y]。
于是起点就是(0,0)，终点是(4,4)。按照刚刚的思路，我们大概手工梳理一遍：
初始条件：
起点Vs为(0,0)
终点Vd为(4,4)
灰色节点集合Q={}
初始化所有节点为白色节点
开始我们的广度搜索！
手工执行步骤【PS：你可以直接看图4-1】:
1.起始节点Vs变成灰色，加入队列Q，Q={(0,0)}
2.取出队列Q的头一个节点Vn，Vn={0,0}，Q={}
3.把Vn={0,0}染成黑色，取出Vn所有相邻的白色节点{(1,0)}
4.不包含终点(4,4)，染成灰色，加入队列Q，Q={(1,0)}
5.取出队列Q的头一个节点Vn，Vn={1,0}，Q={}
6.把Vn={1,0}染成黑色，取出Vn所有相邻的白色节点{(2,0)}
7.不包含终点(4,4)，染成灰色，加入队列Q，Q={(2,0)}
8.取出队列Q的头一个节点Vn，Vn={2,0}，Q={}
9.把Vn={2,0}染成黑色，取出Vn所有相邻的白色节点{(2,1), (3,0)}
10.不包含终点(4,4)，染成灰色，加入队列Q，Q={(2,1), (3,0)}
11.取出队列Q的头一个节点Vn，Vn={2,1}，Q={(3,0)}
12. 把Vn={2,1}染成黑色，取出Vn所有相邻的白色节点{(2,2)}
13.不包含终点(4,4)，染成灰色，加入队列Q，Q={(3,0), (2,2)}
14.持续下去，知道Vn的所有相邻的白色节点中包含了(4,4)……
15.此时获得了答案
起始你很容易模仿上边过程走到终点，那为什么它就是最短的呢？
怎么保证呢？
我们来看看广度搜索的过程中节点的顺序情况：
图4-1 迷宫问题的搜索树
你是否观察到了，广度搜索的顺序是什么样子的？
图中标号即为我们搜索过程中的顺序，我们观察到，这个搜索顺序是按照上图的层次关系来的，例如节点(0,0)在第1层，节点(1,0)在第2层，节点(2,0)在第3层，节点(2,1)和节点(3,0)在第3层。
我们的搜索顺序就是第一层->第二层->第三层->第N层这样子。
我们假设终点在第N层，因此我们搜索到的路径长度肯定是N，而且这个N一定是所求最短的。
我们用简单的反证法来证明：假设终点在第N层上边出现过，例如第M层，M<N，那么我们在搜索的过程中，肯定是先搜索到第M层的，此时搜索到第M层的时候发现终点出现过了，那么最短路径应该是M，而不是N了。
所以根据广度优先搜索的话，搜索到终点时，该路径一定是最短的。
我给出以下代码用于解决上述题目(仅仅只是核心代码)：
/**
* 广度优先搜索
* @param Vs 起点
* @param Vd 终点
*/
bool BFS(Node& Vs, Node& Vd){
queue<Node> Q;
Node Vn, Vw;
int i;
//用于标记颜色当visit[i][j]==true时，说明节点访问过，也就是黑色
bool visit[MAXL][MAXL];
//四个方向
int dir[][2] = {
{0, 1}, {1, 0},
{0, -1}, {-1, 0}
};
//初始状态将起点放进队列Q
Q.push(Vs);
visit[Vs.x][Vs.y] = true;//设置节点已经访问过了！
while (!Q.empty()){//队列不为空，继续搜索！
//取出队列的头Vn
Vn = Q.front();
Q.pop();
for(i = 0; i < 4; ++i){
Vw = Node(Vn.x+dir[i][0], Vn.y+dir[i][1]);//计算相邻节点
if (Vw == Vd){//找到终点了！
//把路径记录，这里没给出解法
return true;//返回
}
if (isValid(Vw) && !visit[Vw.x][Vw.y]){
//Vw是一个合法的节点并且为白色节点
Q.push(Vw);//加入队列Q
visit[Vw.x][Vw.y] = true;//设置节点颜色
}
}
}
return false;//无解
}
为了方便适用于大多数的题解，抽取核心代码如下：
/**
* 广度优先搜索
* @param Vs 起点
* @param Vd 终点
*/
bool BFS(Node& Vs, Node& Vd){
queue<Node> Q;
Node Vn, Vw;
int i;
//初始状态将起点放进队列Q
Q.push(Vs);
hash(Vw) = true;//设置节点已经访问过了！
while (!Q.empty()){//队列不为空，继续搜索！
//取出队列的头Vn
Vn = Q.front();
//从队列中移除
Q.pop();
while(Vw = Vn通过某规则能够到达的节点){
if (Vw == Vd){//找到终点了！
//把路径记录，这里没给出解法
return true;//返回
}
if (isValid(Vw) && !visit[Vw]){
//Vw是一个合法的节点并且为白色节点
Q.push(Vw);//加入队列Q
hash(Vw) = true;//设置节点颜色
}
}
}
return false;//无解
}
对于一个题目来说，要标志节点是否访问过，用数组是一种很快速的方法，但有时数据量太大，很难用一个大数组来记录时，采用hash是最好的做法。实际上visit数组在这里也是充当hash的作用。（PS：至于hash是什么？得自己去了解，它的作用是在O(1)的时间复杂度内取出某个值）
给定序列1 2 3 4 5 6，再给定一个k，我们给出这样的操作：对于序列，我们可以将其中k个连续的数全部反转过来，例如k = 3的时候，上述序列经过1步操作后可以变成：3 2 1 4 5 6 ，如果再对序列 3 2 1 4 5 6进行一步操作，可以变成3 4 1 2 5 6.
那么现在题目就是，给定初始序列，以及结束序列，以及k的值，那么你能够求出从初始序列到结束序列的转变至少需要几步操作吗？
本题可以采用BFS求解，已经给定初始状态跟目标状态，要求之间的最短操作，其实也很明显是用BFS了。
我们把每次操作完的序列当做一个状态节点。那每一次操作就产生一条边，这个操作就是规则。
假设起始节点是：{1 2 3 4 5 6}，终点是：{3 4 1 2 5 6}
去除队列中的起始节点时，将它的相邻节点加入队列，其相邻节点就是对其操作一次的所有序列：
{3 2 1 4 5 6}、{1 4 3 2 5 6}、{1 2 5 4 3 6}、{1 2 3 6 5 4}
然后继续搜索即可得到终点，此时操作数就是搜索到的节点所在的层数2。
题目分类来自网络：
sicily：1048 1444 1215 1135 1150 1151 1114
pku：1136 1249 1028 1191 3278 1426 3126 3087 3414
假设图有V个顶点，E条边，广度优先搜索算法需要搜索V个节点，因此这里的消耗是O(V)，在搜索过程中，又需要根据边来增加队列的长度，于是这里需要消耗O(E)，总得来说，效率大约是O(V+E)。
其实最影响BFS算法的是在于Hash运算，我们前面给出了一个visit数组，已经算是最快的Hash了，但有些题目来说可能Hash的速度要退化到O(lgn)的复杂度，当然了，具体还是看实际情况的。
BFS适合此类题目：给定初始状态跟目标状态，要求从初始状态到目标状态的最短路径。
进而扩展的话就是双向广度搜索算法，顾名思义，即是从起点跟终点分别做广度优先搜索，直到他们的搜索过程中有一个节点相同了，于是就找到了起点跟终点的一条路径。
腾讯笔试题目：假设每个人平均是有25个好友，根据六维理论，任何人之间的联系一定可以通过6个人而间接认识，间接通过N个人认识的，那他就是你的N度好友，现在要你编程验证这个6维理论。
此题如果直接做广度优先搜索，那么搜索的节点数可能达到256，如果是用双向的话，两个树分别只需要搜索到3度好友即可，搜索节点最多为253个，但是用双向广度算法的话会有一个问题要解决，就是你如何在搜索的过程中判断第一棵树中的节点跟第二棵树中的节点有相同的呢？按我的理解，可以用Hash，又或者放进队列的元素都是指向原来节点的指针，而每个节点加入一个color的属性，这样再搜索过程中就可以根据节点的color来判断是否已经被搜索过了。
标签：
原文地址：http://blog.csdn.net/liangzhaoyang1/article/details/51415716
