重拾算法(5)——最小生成树的两种算法及其对比测试

时间：2014-08-01 06:57:11 阅读：394 评论：0 收藏：0 [点我收藏+]

标签：style blog http color 使用 os strong io

重拾算法(5)——最小生成树的两种算法及其对比测试

什么是最小生成树

求解最小生成树(Minimum Cost Spanning Tree，以下简写做MST）是图相关的算法中常见的一个，用于解决类似如下的问题：

假设要在N个城市之间建立通信联络网，那么连通N个城市只需N-1条线路。这时自然会考虑这样一个问题：如何在最节省经费的前提下建立这个通信网。

在任意两个城市间都可以设置一条线路，相应地都要付出一定的经济代价。N个城市之间最多可能设置N(N-1)/2条线路，那么如何在这些线路中选择N-1条，以使总的耗费最少呢？

可以用连通图来表示N个城市，顶点表示城市，通信线路就是带有权值的边。一般而言，一个连通图有多个生成树，这些生成树的总的权值不同，其中会有1或多个的总权值最小，这1或多个生成树就是我们要求解的MST。（只需求出其中一个即可）

本篇介绍两种求解MST的算法：Prim和Kruskal，然后测试之。

Prim算法

现在有一个连通图G，要求MST，我们把G中的顶点划分到U、V两个集合里，假设我们已经知道了MST在U范围内的连接方式，（为什么做这种假设？只可意会不可言传）尚未获知MST在V范围内的连接方式，也不知道MST在U、V之间的连接方式。

现在，我们有办法求得U、V之间的连接方式了：从U、V中分别任取一个顶点（记作u、v），我们知道这有多种取法。U中的顶点有其MST-U，V也有MST-V，而边u-v将MST-U和MST-V的各个顶点都联系起来了，所以MST-U、u-v、MST-V三者就构成了一个生成树ST，而当边u-v是所有取法中最小的那个时，ST自然就是MST了。

整理一下，就是Prim算法的思路：初始时随便取一个顶点vertex作为U，其它顶点作为V。这时，只含有1个顶点的U，其MST-U就是vertex本身，这是已知的。（已经符合假设了）而V范围内的连接方式尚属未知。根据刚刚的推理，我们已经可以求得连接MST-U和MST-V的那条边u-v，顺着u-v，就可以把V中的顶点v拉到U里边。这样重复地拉取顶点，直到V中没有顶点时，U就覆盖了整个G，我们就求得了整个G的MST！

 1     public partial class AdjacencyListGraph<TVertex, TEdge>
 2     {
 3         AdjacencyListGraph<TVertex, TEdge> Prim()
 4         {
 5             if (this.Vertexes.Count == 0) { return null; }
 6 
 7             var result = new AdjacencyListGraph<TVertex, TEdge>();
 8             var firstVertex = this.Vertexes[0].ShallowCopy();// get a copy of this.Vertex[0] without its edges‘ information.
 9             result.Vertexes.Add(firstVertex);// initialize U collection.
10             var VCollection = new List<AdjacencyListVertex<TVertex, TEdge>>(from item in this.Vertexes where item != this.Vertexes[0] select item);// initialize V collection.
11             var this2ResultVertex = new Dictionary<AdjacencyListVertex<TVertex, TEdge>, AdjacencyListVertex<TVertex, TEdge>>();
12             var result2ThisVertex = new Dictionary<AdjacencyListVertex<TVertex, TEdge>, AdjacencyListVertex<TVertex, TEdge>>();
13             this2ResultVertex.Add(this.Vertexes[0], firstVertex);
14             result2ThisVertex.Add(firstVertex, this.Vertexes[0]);
15             while (VCollection.Count > 0)
16             {
17                 AdjacencyListVertex<TVertex, TEdge> u = null;
18                 AdjacencyListEdge<TVertex, TEdge> e = null;
19                 AdjacencyListVertex<TVertex, TEdge> v = null;
20                 foreach (var item in result.Vertexes)
21                 {
22                     var tmpU = result2ThisVertex[item];// get back to ‘this‘ vertex of U
23                     foreach (var tmpE in tmpU.Edges)
24                     {
25                         var tmpV = tmpE.GetTheOtherVertex(tmpU);
26                         if (tmpV != null)
27                         {
28                             if (VCollection.Contains(tmpV))// if (tmpV is in V collection)
29                             {
30                                 if ((e == null) || (tmpE.Weight < e.Weight))
31                                 {
32                                     u = tmpU; e = tmpE; v = tmpV;
33                                 }
34                             }
35                         }
36                         else
37                         {
38                             throw new Exception("Graph has invalid edge!");
39                         }
40                     }
41                 }
42 
43                 if (e != null)
44                 {
45                     var nextVertex = v.ShallowCopy();
46                     result2ThisVertex.Add(nextVertex, v);
47                     this2ResultVertex.Add(v, nextVertex);
48                     var vertex = this2ResultVertex[u];
49                     var edge = new AdjacencyListEdge<TVertex, TEdge>(vertex, nextVertex, e.Weight);
50                     vertex.Edges.Add(edge); nextVertex.Edges.Add(edge);
51                     result.Vertexes.Add(nextVertex);// add new vertex to U collection.
52                     VCollection.Remove(v);// remove v from V collection.
53                 }
54                 else// the graph is not connected!
55                 {
56                     result = null;
57                     break;
58                 }
59             }
60 
61             return result;
62         }
63     }
64     public partial class AdjacencyListEdge<TVertex, TEdge>
65     {
66         public AdjacencyListVertex<TVertex, TEdge> Vertex1 { get;set; }
67         public AdjacencyListVertex<TVertex, TEdge> Vertex2 { get;set; }
68         public virtual int Weight { get;set; }
69 
70         public AdjacencyListVertex<TVertex, TEdge> GetTheOtherVertex(AdjacencyListVertex<TVertex, TEdge> vertex)
71         {
72             if (vertex == null) { return null; }
73             
74             if (this.Vertex1 == vertex) { return this.Vertex2; }
75             else if (this.Vertex2 == vertex) { return this.Vertex1; }
76             else
77             { throw new ArgumentException("edge is not banded to vertex!"); }
78         }
79     }

Prim

Kruskal算法

关于Kruskal（以及任何算法），网上给的反证法、数学归纳法都不适合学习和锻炼算法能力，那些都是在感性认知和灵感走通了迷途之后才适合进行的形而上的东西。

还是按这样的思路来想吧：假设我们已经得到了有N个顶点的图G1的MST-G1，其中G1至少有1个顶点。（又是这种神奇的假设）现在给G1增加一个新顶点v，并用若干条边将v和G1中的某些顶点连接起来。这样我们得到了一个新图G2。与v相连的边中，我们取权值最小的那个（记作v-w），那么MST-G1和v-w加起来就是G2的一个生成树ST。

如果v-w不取最小的那个，那么得到的ST的权值就会增大。如果ST中的MST-G1部分有所改变，那么ST的权值也会增大（或不变）。也就是说，无论我们如何修改ST中的边，ST的权值都不会减小（只会增大或保持不变）。所以ST其实就是G2的最小生成树MST-G2。

由于对G1的约束条件只有"至少有1个顶点"这么一丢丢的限制，那么G2其实可以是任何顶点数V>1的图。

也就是说对于任何顶点数V>1的图G，都可以使用如下方法得到其MST：

设置数组M，用于保存构成MST的边。
在所有未加入M的边中，选取最小的一条边E，如果E满足"E与所有已加入M的边都不构成回路"，就把E加入M。
重复执行上一步，直到标记了V-1条边为止。

注：对于顶点数V=1的图，上述方法也适用。

上述三步就是Kruskal算法。它利用了上文的推理：如果得到了N个顶点的图的MST，就能够得到N+1个顶点的图的MST。这就意味着，我们可以从只有1个顶点的图开始，得到任意有限个顶点的图的MST。它的做法是"每次都尽可能取权值小的边"。这是算法理论中的贪心思想。

注：为了方便进行"选取最小的一条边"这个重复性操作，首先需要对边进行升序排序。

  1     public partial class AdjacencyListGraph<TVertex, TEdge>
  2     {
  3         AdjacencyListGraph<TVertex, TEdge> Kruskal()
  4         {
  5             if (this.Vertexes.Count == 0) { return null; }
  6 
  7             var edgeSorter = new EdgeSorter<TVertex, TEdge>();
  8             var report = this.Traverse(edgeSorter, GraphTraverseOrder.DepthFirst, true);// sort edges.
  9             if (report.ConnectedComponents.Count > 1) { return null; }
 10 
 11             var count = this.Vertexes.Count - 1;
 12             var selectedEdges = new List<AdjacencyListEdge<TVertex, TEdge>>();
 13             var components = new List<List<AdjacencyListVertex<TVertex, TEdge>>>();
 14             foreach (var edge in edgeSorter.sortedEdges)// get selected edges for MST.
 15             {
 16                 if (selectedEdges.Count >= count) { break; }
 17                 TryAddEdge(edge, selectedEdges, components);
 18             }
 19             
 20             var result = GetMST(selectedEdges);
 21             return result;
 22         }
 23         
 24         AdjacencyListGraph<TVertex, TEdge> GetMST(List<AdjacencyListEdge<TVertex, TEdge>> selectedEdges)
 25         {
 26             var result = new AdjacencyListGraph<TVertex, TEdge>();
 27             var this2ResultDict = new Dictionary<AdjacencyListVertex<TVertex, TEdge>, AdjacencyListVertex<TVertex, TEdge>>();
 28             foreach (var vertex in this.Vertexes)// get vertexes for MST.
 29             {
 30                 var newVertex = vertex.ShallowCopy();
 31                 this2ResultDict.Add(vertex, newVertex);
 32                 result.Vertexes.Add(newVertex);
 33             }
 34 
 35             foreach (var selected in selectedEdges)// get edges for MST.
 36             {
 37                 var v1 = this2ResultDict[selected.Vertex1];
 38                 var v2 = this2ResultDict[selected.Vertex2];
 39                 var newEdge = new AdjacencyListEdge<TVertex, TEdge>(v1, v2, selected.Weight);
 40                 v1.Edges.Add(newEdge);
 41                 v2.Edges.Add(newEdge);
 42             }
 43             return result;
 44         }
 45         
 46         bool TryAddEdge(AdjacencyListEdge<TVertex, TEdge> edge, List<AdjacencyListEdge<TVertex, TEdge>> selectedEdges, List<List<AdjacencyListVertex<TVertex, TEdge>>> components)
 47         {
 48             List<AdjacencyListVertex<TVertex, TEdge>> component1 = null;
 49             List<AdjacencyListVertex<TVertex, TEdge>> component2 = null;
 50             foreach (var component in components)
 51             {
 52                 foreach (var v in component)
 53                 {
 54                     if (v == edge.Vertex1)
 55                     { component1 = component; }
 56                     if (v == edge.Vertex2)
 57                     { component2 = component; }
 58                 }
 59             }
 60             if (component1 != null)
 61             {
 62                 if (component2 != null)
 63                 {
 64                     if (component1 == component2)
 65                     { return false; }
 66                     else
 67                     {
 68                         component1.AddRange(component2);
 69                         components.Remove(component2);
 70                         selectedEdges.Add(edge);
 71                         return true;
 72                     }
 73                 }
 74                 else
 75                 {
 76                     component1.Add(edge.Vertex2);
 77                     selectedEdges.Add(edge);
 78                     return true;
 79                 }
 80             }
 81             else
 82             {
 83                 if (component2 != null)
 84                 {
 85                     component2.Add(edge.Vertex1);
 86                     selectedEdges.Add(edge);
 87                     return true;
 88                 }
 89                 else
 90                 {
 91                     var component = new List<AdjacencyListVertex<TVertex, TEdge>>();
 92                     component.Add(edge.Vertex1);
 93                     component.Add(edge.Vertex2);
 94                     components.Add(component);
 95                     selectedEdges.Add(edge);
 96                     return true;
 97                 }
 98             }
 99         }
100     }

Kruskal

对边排序我使用了折半插入排序。

 1     public class EdgeSorter<TVertex, TEdge> : GraphNodeWorker<TVertex, TEdge>
 2     {
 3         public IList<AdjacencyListEdge<TVertex, TEdge>> sortedEdges = new List<AdjacencyListEdge<TVertex, TEdge>>();
 4         int count = 0;
 5         public override void DoActionOnNode(AdjacencyListVertex<TVertex, TEdge> vertex)
 6         {
 7             if (vertex == null) { return; }
 8             foreach (var edge in vertex.Edges)
 9             {
10                 if (!sortedEdges.Contains(edge))
11                 {
12                     InsertElement(edge);
13                 }
14             }
15         }
16         // optimized verstion of InsertElement() method.
17         void InsertElement(AdjacencyListEdge<TVertex, TEdge> element)
18         {
19             var min = 0;
20             var max = count - 1;
21             while (min <= max)
22             {
23                 var middle = (min + max) / 2;
24                 if (element.Weight - this.sortedEdges[middle].Weight < 0)
25                 { max = middle - 1; }
26                 else
27                 { min = middle + 1; }
28             }
29 
30             this.sortedEdges.Insert(min, element);
31             count++;
32         }
33 
34         /* this is the original version which is not optimized.
35         void InsertElement(AdjacencyListEdge<TVertex, TEdge> element)
36         {
37             if (count == 0) { this.sortedEdges.Add(element); return; }
38             var min = 0;
39             var max = count - 1;
40             var middle = 0;
41             var compare = 0;
42             while (min <= max)
43             {
44                 middle = (min + max) / 2;
45                 compare = element.Weight - sortedEdges[middle].Weight;
46                 if (compare < 0)
47                 { max = middle - 1; }
48                 else
49                 { min = middle + 1; }
50             }
51             if (compare < 0)
52             {
53                 this.sortedEdges.Insert(middle, element);//(min) equals (middle) equals (max + 1)
54             }
55             else
56             {
57                 this.sortedEdges.Insert(middle + 1, element);//(min) equals (middle + 1) equals (max + 1)
58             }
59             count++;
60         }
61         */
62     }

对比测试

实现了Prim和Kruskal算法后，就该测试一下他们的正确性了。思考了2天后，我认为如下方案既简单可行又有足够的说服力：仍旧用上一篇的方法自动生成顶点数为1、2、3、4、5、6的所有图的形态，并对其边随机赋予权值；然后对得到的每一个图G，分别用Prim和Kruskal算法计算MST；然后对比两种算法得到的MST的总权值是否相同；如果不同，就说明至少有一个算法的代码有问题；如果对所有情形的图的计算，其Prim和Kruskal得到的MST权值都分别相同，那就很强地说明代码没问题。由于各个边的权值是随机给的，可以通过多次重复测试的方式，进一步加强说明代码的正确性。

这种逼近式的对比测试，其实现很容易且说服力很强；同时，真正的完全测试我实在精力不足，这决定了我采用如上所述的测试策略。

测试思路已经给出了，代码也简单地很，下面只给出一个测试用例作为示例。

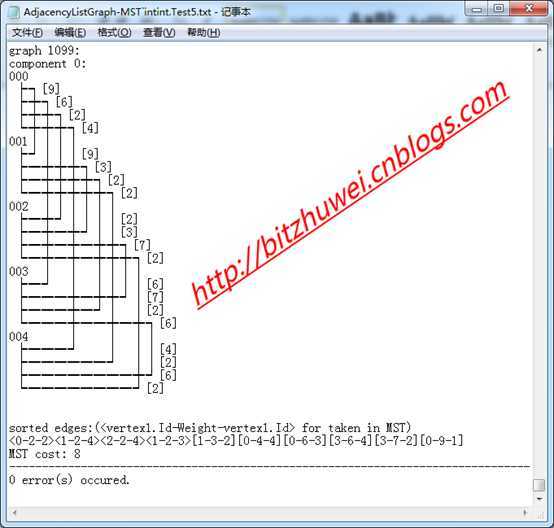
bubuko.com,布布扣