标签:style blog http color os io 2014 art
明天是七夕,中国的情人节,为了应节,这一篇提供几个心形曲面的算法.
说到心形,我想到一个笑话,有个女老师在黑板上画了个心形图案,问学生加:"这是什么?"学生们回答:"屁股."老师气哭了,去找校长理论.校长来了就批评学生:"你们怎么又的把老师给气哭了呢?"然后看到了黑板上的图案继续说道:"你们也太调皮了,怎么还在黑板上画了个屁股呢!"
好笑吧,其实我也有类似的经历,有人曾对我说:"你怎么拿个屁股做博客园的头像呢?"我只好无奈的回答:"这不是屁股,这是心形,而且这个心形是我用程序画出来的."关于我的心形头像生成的算法,请看我之前发的博客:屏保:画线圈LineFlower, 3D屏保: 线圈, WhyDemo: 画线圈LineFlower.

我前几天还发过一篇博客:数学图形(1.4)心形线
关于心形曲面,我查找一些资料,但都是隐式方程的曲面,即给出一个数学方程式,然后说这个方程所表示的图形即是一个心形曲面.对于隐式方程,我以后有机会再详细介绍.我从网上下了一个隐式方程解析的代码.不太好用,运算时间很长,图形的顶点分布有些错乱.如下图所示:


我的软件工具目前只能处理显示方程的曲面.下面将发布我所写的几个心形曲面的算法脚本代码:
(1)heart(圆变)
这是我在球曲面的基础上变换出来的.
vertices = dimension1:80 dimension2:160 a = from 0 to (2*PI) dimension1 b = from (-PI*0.5) to (PI*0.5) dimension2 r = 10.0 c = sqrt(abs(a - PI))*1.5 x = r*cos(b)*sin(a)*c y = -r*cos(b)*cos(a)*c z = r*sin(b)*0.75 u = a v = b*2 y = y - array_min(y)*0.5

(2)尖尖的心形
曲线:
vertices = 1000 r = 10.0 t = from 0 to (2*PI) p = sin(t)*sqrt(abs(cos(t)))/(sin(t) + 7/5) - 2*sin(t) + 2 x = p*sin(t) y = p*cos(t)
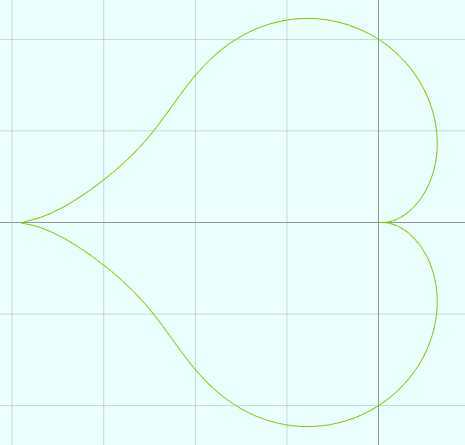
曲面:
vertices = D1:360 D2:100 r = 10.0 u = from 0 to (2*PI) D1 v = from (-PI/2) to (PI/2) D2 p = sin(u)*sqrt(abs(cos(u)))/(sin(u) + 7/5) - 2*sin(u) + 2 x = p*cos(u) y = p*sin(u) + 1.5 x = x*cos(v) y = y*cos(v) z = 0.8*sin(v)

(3)完美的心形
这是我目前生成的最完美的心形
曲线:
vertices = 360 u = from (-PI) to (PI) w = abs(u) p = w*sqrt(w/(1 + w)) x = p*sin(u) y = (p*cos(u) + 1)*0.9

平面:
vertices = D1:360 D2:100 u = from (-PI) to (PI) D1 v = from 1 to 100 D2 w = abs(u) p = w*sqrt(w/(v + w)) x = p*sin(u) y = p*cos(u)*0.9

曲面:
vertices = D1:360 D2:64 u = from (-PI) to (PI) D1 v = from (PI/2) to (-PI/2) D2 w = abs(u) p = w*sqrt(w/(1 + w)) b = 0.5 x = p*sin(u)*cos(v) y = (p*cos(u) + 0.9)*0.9*cos(v) z = b*sin(v)

如果你觉得这个心形还是像屁股,那你与下面的图形比较下,就会发现不像了.
(4)像屁股的心形
#http://xahlee.info/surface/kuen/kuen.html vertices = D1:100 D2:100 u = from (-1.4325*PI) to (1.4325*PI) D1 v = from (-10) to (10) D2 w = (cosh[v]^2 + u^2) x = 2*cosh[v]*(cos[u] + u*sin[u]) z = 2*cosh[v]*(-u*cos[u] + sin[u]) y = v - (2*sinh[v]*cosh[v]) x = x/w y = y/w z = z/w

标签:style blog http color os io 2014 art
原文地址:http://www.cnblogs.com/WhyEngine/p/3885126.html