标签:
Content
10. Dimensionality Reduction
10.1 Motivation
10.1.1 Motivation one: Data Compression
10.2.2 Motivation two: Visualization
10.2 Principal Component Analysis
10.2.1 Problem formulation
10.2.2 Principal Component Analysis Algorithm
10.2.3 Choosing the Number of Principal Components
10.2.4 Advice for Applying PCA
如果我们有许多冗余的数据,我们可能需要对特征量进行降维(Dimensionality Reduction)。
我们可以找到两个非常相关的特征量,可视化,然后用一条新的直线来准确的描述这两个特征量。例如图10-1所示,x1和x2是两个单位不同本质相同的特征量,我们可以对其降维。
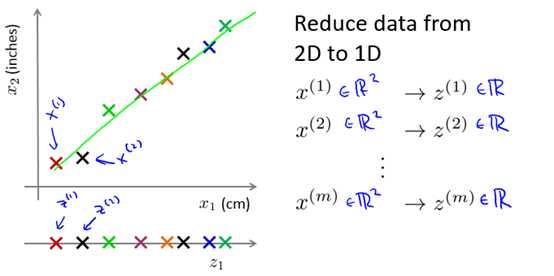
图10-1 一个2维到1维的例子
又如图10-2所示的3维到2维的例子,通过对x1,x2,x3的可视化,发现虽然样本处于3维空间,但是他们大多数都分布在同一个平面中,所以我们可以通过投影,将3维降为2维。
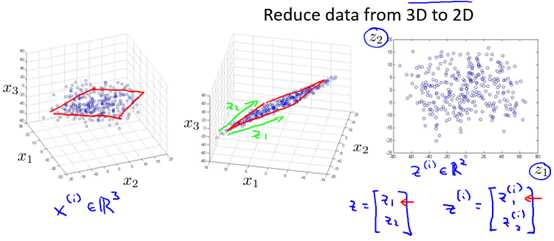
图10-2 一个3维到2维的例子
降维的好处很明显,它不仅可以数据减少对内存的占用,而且还可以加快学习算法的执行。
注意,降维只是减小特征量的个数(即n)而不是减小训练集的个数(即m)。
我们可以知道,但特征量维数大于3时,我们几乎不能对数据进行可视化。所以,有时为了对数据进行可视化,我们需要对其进行降维。我们可以找到2个或3个具有代表性的特征量,他们(大致)可以概括其他的特征量。
例如,描述一个国家有很多特征量,比如GDP,人均GDP,人均寿命,平均家庭收入等等。想要研究国家的经济情况并进行可视化,我们可以选出两个具有代表性的特征量如GDP和人均GDP,然后对数据进行可视化。如图10-3所示。
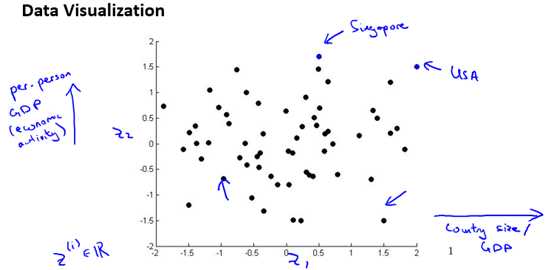
图10-3 一个可视化的例子
主成分分析(Principal Component Analysis : PCA)是最常用的降维算法。
首先我们思考如下问题,对于正交属性空间(对2维空间即为直角坐标系)中的样本点,如何用一个超平面(直线/平面的高维推广)对所有样本进行恰当的表达?
事实上,若存在这样的超平面,那么它大概应具有这样的性质:
下面我们以3维降到2维为例,来试着理解为什么需要这两种性质。图10-4给出了样本在3维空间的分布情况,其中图(2)是图(1)旋转调整后的结果。在10.1节我们默认以红色线所画平面(不妨称之为平面s1)为2维平面进行投影(降维),投影结果为图10-5的(1)所示,这样似乎还不错。那为什么不用蓝色线所画平面(不妨称之为平面s2)进行投影呢? 可以想象,用s2投影的结果将如图10-5的(2)所示。
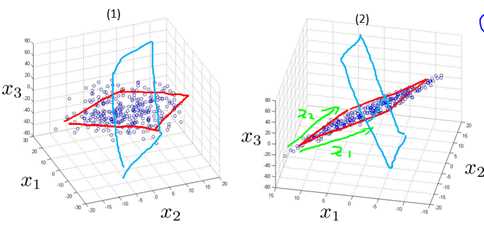
图10-4 样本在3维正交空间的分布
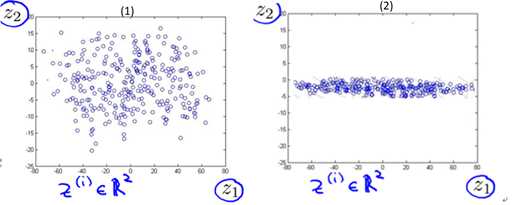
图10-5 样本投影在2维平面后的结果
由图10-4可以很明显的看出,对当前样本而言,s1平面比s2平面的最近重构性要好(样本离平面的距离更近);由图10-5可以很明显的看出,对当前样本而言,s1平面比s2平面的最大可分性要好(样本点更分散)。不难理解,如果选择s2平面进行投影降维,我们会丢失更多(相当多)的特征量信息,因为它的投影结果甚至可以在转化为1维。而在s1平面上的投影包含更多的信息(丢失的更少)。
这样是否就是说我们从3维降到1维一定会丢失相当多的信息呢? 其实也不一定,试想,如果平面s1投影结果和平面s2的类似,那么我们可以推断这3个特征量本质上的含义大致相同。所以即使直接从3维到1维也不会丢失较多的信息。这里也反映了我们需要知道如何选择到底降到几维会比较好(在10.2.3节中讨论)。
让我们高兴的是,上面的例子也说明了最近重构性和最大可分性可以同时满足。更让人兴奋的是,分别以最近重构性和最大可分性为目标,能够得到PCA的两种等价推导。
一般的,将特征量从n维降到k维:
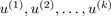 ,将所有样本投影到这k个向量构成的超平面,使得投影的距离最小(或者说投影误差projection error最小)。
,将所有样本投影到这k个向量构成的超平面,使得投影的距离最小(或者说投影误差projection error最小)。 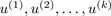 ,将所有样本投影到这k个向量构成的超平面,使得样本点的投影能够尽可能的分开,也就是使投影后的样本点方差最大化。
,将所有样本投影到这k个向量构成的超平面,使得样本点的投影能够尽可能的分开,也就是使投影后的样本点方差最大化。 注意: PCA和线性回归是不同的,如图10-6所示,线性回归是以平方误差和(SSE)最小为目标,参见1.2.4节;而PCA是使投影(二维即垂直)距离最小;PCA与标记或者预测值完全无关,而线性回归是为了预测y的值。
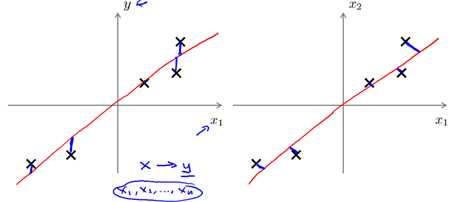
图10-6 PCA不是线性回归
分别基于上述两种目标的具体推导过程参见周志华老师的《机器学习》P230。两种等价的推导结论是:对协方差矩阵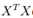 进行特征值分解,将求得的特征值进行降序排序,再去前k个特征值对应的特征向量构成
进行特征值分解,将求得的特征值进行降序排序,再去前k个特征值对应的特征向量构成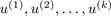 。
。
其中
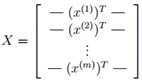
基于上一节给出的结论,下面给出PCA算法。
输入:训练集: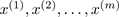 ,低维空间维数k
,低维空间维数k
过程:
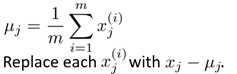
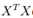 (Sigma)
(Sigma) 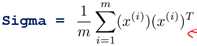 (其中
(其中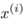 是n*1的向量)
是n*1的向量)
在matlab中具体实现如下,其中X为m*n的矩阵:
Sigma = (1/m) * X‘* X;
在实践中通常对协方差矩阵进行奇异值分解代替特征值分解。在matlab中实现如下:
[U, S, V] = svd(Sigma); (svd即为matlab中奇异值分解的内置函数)
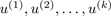
在matlab具体实现时,Ureduce = 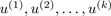 认为是第3步求得的U的前k个,即有:Ureduce = U( : , 1:k); 其中Ureduce为n*k的矩阵
认为是第3步求得的U的前k个,即有:Ureduce = U( : , 1:k); 其中Ureduce为n*k的矩阵
经过了上述4步得到了投影矩阵Ureduce,利用Ureduce就可以得到投影后的样本值
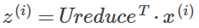 (
(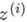 为k*1的向量)
为k*1的向量)
下面总结在matlab中实现PCA的全部算法(假设数据已被中心化)
Sigma = (1/m) * X‘ * X; % compute the covariance matrix
[U,S,V] = svd(Sigma); % compute our projected directions
Ureduce = U(:,1:k); % take the first k directions
Z = Ureduce‘ * X; % compute the projected data points
如何选择k(又称为主成分的个数)的值?
首先,试想我们可以使用PCA来压缩数据,我们应该如何解压?或者说如何回到原本的样本值?事实上我们可以利用下列等式计算出原始数据的近似值Xapprox:
Xapprox = Z * Ureduce (m*n = m*k * k*n )
自然的,还原的数据Xapprox越接近原始数据X说明PCA误差越小,基于这点,下面给出选择k的一种方法:

结合PCA算法,选择K的算法总结如下:

这个算法效率特别低。在实际应用中,我们只需利用svd()函数,如下:
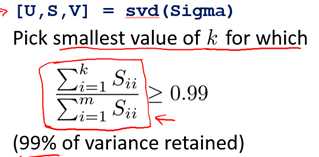
参考:《机器学习》 周志华
Stanford机器学习笔记-10. 降维(Dimensionality Reduction)
标签:
原文地址:http://www.cnblogs.com/llhthinker/p/5522054.html