标签:
数据结构——栈
前言:
大家好,以后会上传数据结构的一系列解题记录和学习记录,谢谢大家的关注。
(限于本人的经验,如此博文有谬误之处,请及时评论,谢谢大家)
正文:
第一天:
今天我学了栈(其实早就会),正好心血来潮要写写数据结构的学习记录,所以就写了这个博文,不明白为什么上篇博文为什么有那么多人阅读,希望继续关注。
好了,直接开门见山吧,今天要讲的是以下几条:
1.栈是什么?
2.栈的操作函数
3.栈的应用详细说明
4.题目中栈的应用
下面进入第一条:栈是什么?
对,栈是什么?
那么,你见过死胡同吗?现在城市的车越来越多,比方说,你晚上开车九点钟回家,如果没有车位的话,你第一个想法是把车放哪?反正我会想把车堵在外面,挡在明天不走的车前面。
示意图就是这样:
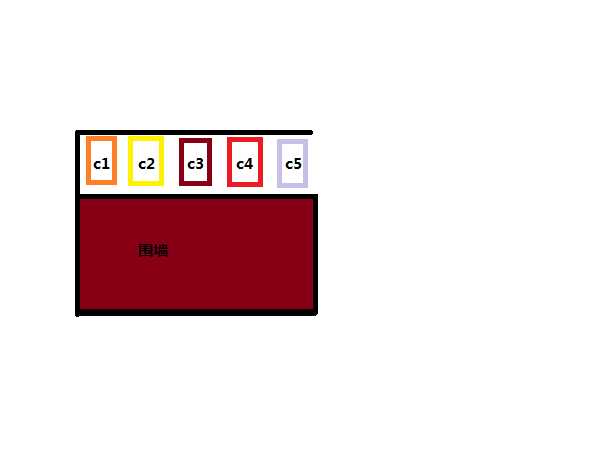
很显然,假设车头在右边,c1是最先进的,但是,c1要等到c5、c4、c3、c2先全部出来以后,才能出来,所以,栈这个线性结构具有一个非常实用的特性——先进后出,这让stack成为做题的非常实用的工具。
你可以把这个stack想象成一个“死胡同”,只要你前面的元素不出来,或不被“pop”掉的话,你就不会被读取,就像你在一个箱子里拿小包袱一样。
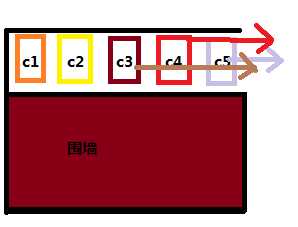
栈的定义如下:
首先 系统或者数据结构栈中数据push和pop 是两回事!
插入是增加数据 弹出 是删除数据 ,这些操作只能从栈顶即最低地址作为约束的接口界面入手操作 ,但读取栈中 的数据 是随便的 没有接口约束之说。很多人都误解这个理念从而对栈产生困惑。而系统栈在计算机体系结构中 又起到一个跨部件交互的媒介区域的作用 即 cpu 与内存的交流通道 ,cpu只从系统给我们自己编写的应用程序所规定的栈入口线性地读取执行指令, 用一个形象的词来形容它就是pipeline。
cpu内部交互具体参见 EU与BIU的概念介绍。(转自360)
栈作为一种数据结构,是一种只能在一端进行插入和删除操作的特殊线性表。它按照后进先出的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶。
需要读数据的时候从栈顶开始弹出数据(最后一个数据被第一个读出来)。栈具有记忆作用,对栈的插入与删除操作中,不需要改变栈底指针。
栈是允许在同一端进行插入和删除操作的特殊线性表。允许进行插入和删除操作的一端称为栈顶(top),另一端为栈底(bottom);
栈底固定,而栈顶浮动;栈中元素个数为零时称为空栈。
插入一般称为进栈(PUSH),删除则称为退栈(POP)。栈也称为后进先出表。
第二天:
2.栈的操作函数
栈的操作函数?系统提供吗?还是要自己写一个stack(栈)的模板类?
学数据结构,就要知道STL,STL是一个功能特别强大的东西,但你肯定不能偷偷摸摸去调用它的public函数,当然首先要#include<数据结构名>,本章中,是#include<stack>,其中包括了stack需要使用的绝大部分的函数。
定义:
定义方法如下:
stack<int/char/bool....> s/*(stack名称,当然了,不一定是s)*/;
还可以这样定义:
char/int/bool..... s[10000];//模拟一个栈
主要函数:
 stack
stack
1. s.push(int/char...... n):
功能正如push一样,就是把一个元素推入栈中,也就是推入现在深度最深且有位置的那个位置
注意事项及运行过程:
①若TOP≥n时,则给出溢出信息,作出错处理(进栈前首先检查栈是否已满,满则溢出;不满则②);
②置TOP=TOP+1(栈指针加1,指向进栈地址);
③S(TOP)=n,结束(n为新进栈的元素);
2. s.pop():
pop:弹出,顾名思义就是弹出栈顶的元素,为动作函数,随即top减一。
注意事项及运行过程:
①若TOP≤0,则给出下溢信息,作出错处理(退栈前先检查是否已为空栈, 空则下溢;不空则作②);
②X=S(TOP),(退栈后的元素赋给X):
③TOP=TOP-1,结束(栈指针减1,指向栈顶)。
3. s.size()
这个当然是返回栈的大小了。
4. s.top()
这个函数正好跟pop函数相反,它用top指针访问栈顶元素,但不弹出。
5. empty()
判断栈是否为空,真则返回1,反之返回0
操作实例:
stack<int> s;
操作 | 栈 | 输出
empty() | | true
push(7) | 7 | 无
push(2) | 7 2 | 无
top () | 7 2 | 2
pop() | 7 | 2
empty()| 7 | false
size() | 7 | 1
 View Code
View Code
3.栈的应用详细说明
栈的应用广泛,其原因就是拥有上面提到过的先进后出,后进先出的特点。
栈可以应用在很多题目当中
例如 进制转换等题目。
下面将给出例题和详解。
4.题目中栈的应用
一道典型的栈题:
| 栈:括号匹配问题 |
| 难度级别:B; 运行时间限制:1000ms; 运行空间限制:51200KB; 代码长度限制:2000000B |
|
试题描述
|
|
给定一个只含有大小括号的字符串,请你判断这个字符串里括号使用是否正确。括号的用法跟数学上唯一不同的是大中小括号没有级别的区分。例如 ((){([])}) 是正确的字符串,而 )([()] 就是错误的。 |
|
输入
|
|
一个只包含大中小括号的字符串,字符串长度不会超过 1000 。
|
|
输出
|
|
yes 或 no。如果括号使用正确就输出 yes,如果使用错误就输出 no 。
|
|
输入示例
|
|
((){([])})
|
|
输出示例
|
|
yes
|
这道题第一个反应,当然是用栈结构,但具体怎么用呢?
1.遇到一个括号判断,是左括号的就让它入栈,不是的话就看栈顶上那个元素是不是对应的前括号,要不是,就直接return 0;
2.如果是,则将栈顶元素弹出。
3.判断栈高度是否为0,非则输出no,是则输出yes。
 View Code
View Code
还可以这样做(转载)
 View Code
View Code
栈还是很简单的,只要细细学习就会发现:它是数据结构中最简单的之一。
标签:
原文地址:http://www.cnblogs.com/wxjor/p/5535784.html