标签:
Dijkstra
太多文章了,有些简练,有些一笔带过.自己还是花了些时间才明白,刚脆自己写个图文说明的,希望能让还没明白的,尽快清楚.
问题:求某点到图中其他所有点的最短路径(权值和最小)
Dijkstra.其实只有4个数据和3句话。明白了这3句话,这个算法就理解了。
第一个数据:还未到达的点的集合。noDone{顶点编号,权值} 顶点编号 和 原点到此编号最小权的候选值
第二个数据:源点 sourceVertex
第三个数据:最新到达的点 lastestVertex
第四个数据:最新到达的点的权 lVCost
第一句话:初始化noDone,把所有除源点之外的点,加入到nodne中。权为这个点直连原点的权,无直线设置为无限大int_max.
第二句话:如果noDone中还有数据,找出noDone中权直最小的点,并把这个点作为 lastestVertex,把它的权作为lVCost,顺便把它从noDone中删除
第三句话:更新noDone中的每个元素的权值,重复第二句话。
分析之前先看流程:
第一句话:初始化noDone,把所有除源点之外的点,加入到nodne中。权为这个点直连原点的权,无直线设置为无限大int_max.
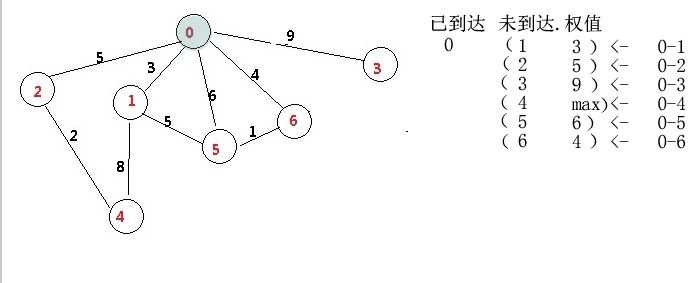
完成后3个数据
noDone:(1,3)(2,5)(3,9)(4,max)(5,6)(6,4)
sourceVertex:0
lastestVertex:可以设置为sourceVertex的值。
lVCost:0
第二句话:如果noDone中还有数据,找出noDone中权直最小的点,并把这个点作为 lastestVertex,把它的权作为lVCost,顺便把它从noDone中删除
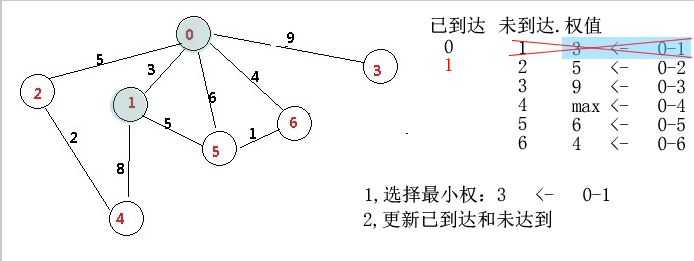
执行前数据:
noDone:(1,3)(2,5)(3,9)(4,max)(5,6)(6,4)
sourceVertex:0
lastestVertex:0
lVCost:0
(1,3)这个最小,点为1,权为3。
lastestVertex,更新为1
执行后数据:
noDone:(2,5)(3,9)(4,max)(5,6)(6,4)
sourceVertex:0
lastestVertex:1
lVCost:3
第三句话:更新noDone中的每个元素的权值,重复第二句话。
执行前数据:
noDone:(2,5)(3,9)(4,max)(5,6)(6,4)
sourceVertex:0
lastestVertex:1
lVCost:3
如何更新,比较2个值看谁小。第一个值:点到原点的权。第二个值:点到lastestVertex的权+lVCost。
比如:4点,到原点的权为无限大,到1点的权为8+3(lVCost)=11。11更小。所以(4,max)更新为(4,11)。
这里其实只需要更新和lastestVertex相连的点,就可以。因为和lastestVertex不相连,那么肯定是原来的直更小,或相等。
执行后数据:
noDone:(2,5)(3,9)(4,11)(5,6)(6,4)
sourceVertex:0
lastestVertex:1
lVCost:3
分析和思索:
源点到达某个点可以有很多路径,除非列出所有可能路径,再比较才能得出结果.
是的,但有一个特例,就是和原点直联的所有点中,权直最小的那个点.暂且叫最近点.
如图中,权直最小的是3, 1为最近点.
我们马上就可以确定0->1这条路径,就是0和1的最短路径。
如何证明:
反证法:假如有 0->x-->1是最优路径.首先0->x就大于等于 3,因为从0出发,已经确定了0—>1最小。
式子观察法:最优路径无非就是 x+y+z+...=总权值。x是从原点出发直连的路径。y是点的第二条路...总权值最小。就是去掉y,去掉z,找x最小的。就找到了所有最优路径中的最小的路径。
想明白这个,才能继续往下处理。所以直连中,权最小的那个,已经确定了最优路径。权值就是直连路径的权。
看一看,上面的分析已经解释了3句话中的2句了。
第一句话:初始化noDone,把所有除源点之外的点,加入到nodne中。权为这个点直连原点的权,无直线设置为无限大int_max.
第二句话:如果noDone中还有数据,找出noDone中权直最小的点,并把这个点作为 lastestVertex,把它的权作为lVCost,顺便把它从noDone中删除
解释第三句话前先分析:
如果纯粹继续贪心思路,可以得到另外一种解决方案,这是我在理解 Dijkstra.之前自己想出的思路。 可以看下自己笨拙的思路和别人的对比。
我们先假设找出了原点到各个点的最短路径。那么第二条最短路径肯定是比第一条长,但比第三条短。废话!
比第一条长,但比第三条短,在哪里呢?有2个地方,可供候选。
1)继续从原点出发,找出除掉刚才找到的,第2长的。也就是0-》6。
2)从新顶点1出发,找出最短的。也就是0-》1-》5。 比较0-》6和0-》1-》5,谁的权直更小。就完成了。
没有其他可能了吗?为什么?
首先只要把0->6作为下一个最短路径的候选, 那么0->2,0->3,0->4,0->5,以及由他们产生的路径,就比0-》6长。
唯一的可能,就是曾经的最优路线0->1,基础上,走下一个点。
思路是这样,没错,但Dijkstra为什么归纳在动态算法中。
Dijkstra这个时候,并没有直接找下一个最短路径,而选择 更新和lastestVertex相连的点 的权。动态调整 每个点到 原点的 目前所能确定的最小权直。
以方便他回到第二句话。找到新的最短路径。找到后,继续更新和lastestVertex相连的点 的权,每次都更新,每个点到 原点的 目前所能确定的最小权直。
步步逼近,步步找出最小的那个。只有最小的才是确定的。最小的那个没有可能再小了,但其他的有可能在这个最小的基础上,饶个弯过来。比原来node中的权直更小。
哎,这里总感觉说不明白,虽然自己明白。
写下来把。 任何最短路径的产生,只可能是在原来所有最短路径的基础上,贪心的比较。
这里要把原点到原点也当成一条最短路径。原点的最短路径就是0->0,
我们只需要有新的最优顶点,更新和最优顶点相连的点,再来最优顶点。再更新和 这个最优顶点相连的点,上一次的最优顶点的不用管了,因为上次已经更新了。而且没次都会比较,保存最小的。
所有的noDone中的权直,都是他本身的最小候选值,不是最终最优路径的权直,但是每次最小的那个权直不单是候选值,而且是最终最小权直。
看来还是贴公式更简洁。
代码 c。
struct distance { int noGet; int dist; }; int main() { int matrix[7][7]={ 0,3,5,9,0x7fffffff,6,4, 3,0,0x7fffffff,0x7fffffff,8,5,0x7fffffff, 5,0x7fffffff,0,0x7fffffff,2,0x7fffffff,0x7fffffff, 9,0x7fffffff,0x7fffffff,0,0x7fffffff,0x7fffffff,0x7fffffff, 0x7fffffff,8,2,0x7fffffff,0,0x7fffffff,0x7fffffff, 6,5,0x7fffffff,0x7fffffff,0x7fffffff,0,1, 4,0x7fffffff,0x7fffffff,0x7fffffff,0x7fffffff,1,0 }; int minTop=0; struct distance noG[6]= { {1,3},{2,5},{3,9},{4,0x7fffffff},{5,6},{6,4} }; int count_minRd=1; int i=0; while(count_minRd<7) { int shortest=0x7fffffff; int shortest_i=0; for(i=0;i<6;i++) { if(noG[i].noGet!=-1) { if(noG[i].dist<=shortest) { shortest_i=i; shortest=noG[i].dist; } } } minTop=shortest_i;//更新刚找出的最短路径的顶点。 printf("0->....->%d cost:%d\n",minTop+1,shortest); noG[shortest_i].noGet=-1;//简单的赋直为-1,表示删除。 //动态更新,剩下未处理的点的权值。,对比到源点和到新顶点+新顶点本身权值,取小值。 for(i=0;i<6;i++) { if(noG[i].noGet!=-1) { int i_n=i+1; int i_t=minTop+1; int newCost=0x7fffffff;//只有相联,才需要更新,因为只有相连的权值才会发生变化。 if(matrix[0,i_n]<matrix[i_n][i_t]+noG[shortest_i].dist && matrix[i_n][i_t]!=0x7fffffff) { newCost=matrix[0,i_n]; } else if(matrix[0][i_n]>matrix[i_n][i_t]+noG[shortest_i].dist && matrix[i_n][i_t]!=0x7fffffff) { newCost=matrix[i_n][i_t]+noG[shortest_i].dist; } if(newCost<noG[i].dist) { noG[i].dist=newCost; } } } count_minRd++; } return 0; }
标签:
原文地址:http://www.cnblogs.com/lsfv/p/5534883.html