形状特征-HU矩

标签：

p+q阶矩:具有两个边缘的游街函数f(x,y)的p+q阶矩m_pq定义为

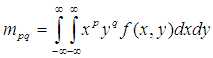
式中,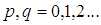,即p和q可取所有的非负整数值,因此产生一个矩的无限集,而且该集合完全可以确定函数f(x,y)本身.换句话说,函数与其矩集合有一个一一对应的关系:集合{m_pq}对于函数f(x,y)是唯一的,也只有f(x,y)才具有该特定的矩集.

对于大小为MxN的数字图像f(i,j)的p+q阶矩为

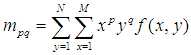
0阶矩 只有一个m₀₀,m₀₀是图像各像素灰度的综合,二值图像的m₀₀则表示目标物体的面积.1阶矩有两个,高阶矩则更多.用0阶矩除所有的1阶矩和高阶矩可以使他们和物体的大小无关.

如果用m₀₀来归一化1阶矩m₁₀和m₀₁,则得到目标物体的质心(即形心)坐标:

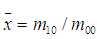
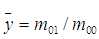
中心矩可以以质心作为原点进行计算的:

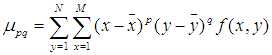
为获得缩放午饭的性质,可以对中心矩进行归一化操作,即把上述中心矩用0阶中心矩来归一化,叫做归一化中心距:

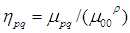
其中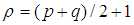;p+q=2,3,4...

相对于主轴计算并用面积归一化的中心矩,在物体放大,平移和旋转时保持不变.单纯的中心矩尽管可以表征平面物体的几何形状,但都不具备不变形,但可以由这些矩构造不变量.这种方法最初是由Ming-Kuei Hu在1962年提出的,他利用归一化2阶和3阶中心矩,到处7个局域变换,旋转和缩放无关性的矩(Hu不变矩):

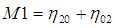
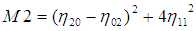
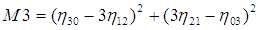
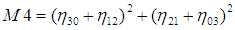
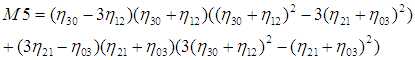
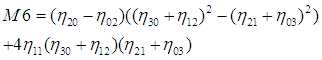
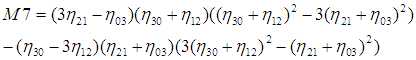
利用不变矩的目标识别算法课按一下步骤进行:

1. 读初始目标图像和测试图像进行预处理,将目标从背景中分割出来,将灰度图像转换为二值图像;
2. 提取目标的边缘,并计算目标区域和边界的中心矩;
3. 对上述两组中心矩进行归一化,在归一化的基础上计算出7个不变矩M1~M7,共同组成目标图像和测试图像中目标的特征向量;
4. 计算两个向量之间的欧式距离D,即为目标图像和测试图像的归一化特征向量的欧式距离.预先设定一个阈值L,以确定两者的相似度,如果D<L,则测试图像中的目标是要寻找的目标,反之则不是.

形状特征-HU矩

标签：

原文地址：http://www.cnblogs.com/brainit/p/5539548.html