标签:codeforces round #25
传送门:点击打开链接
解题思路:
水题,推出公式,直接打印即可。
代码:
#include <cstdio>
#include <cstring>
using namespace std;
int main()
{
int n;
scanf("%d", &n);
for(int i = 1; i <= n; ++i)
{
if(i <= n/2)
{
int t = (n+1-2*i)/2;
for(int j = 0;j< t; ++j)
printf("*");
for(int j = 0; j < 2*i-1; ++j)
printf("D");
for(int j=0; j<t; ++j)
printf("*");
printf("\n");
}
else
{
int w = 2*n+1-2*i, t = (n-w)/2;
for(int j = 0; j < t; ++j)
printf("*");
for(int j = 0; j <w; ++j)
printf("D");
for(int j = 0; j < t; ++j )
printf("*");
printf("\n");
}
}
return 0;
}
题意:
给一个序列,每次可以把序列的最后一个数移到最前面,如果可以使序列递增(严格来说是非递减),输入最少移动次数,否则,输出-1;
解题思路:
先将序列扫一遍,遇到非递增的位置(记为t)跳出,接着从从t+1开始扫一遍,如果,后面的序列递增,则输出其长度,即为答案,否则,输出-1。因为如果要按照题中所述方式移动,使序列变为递增,序列应当是本来就是递增的,或者是可以分为两个连续的递增子序列的。
传送门:点击打开链接
代码:
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int MAXN = 1e5 + 10;
int n, a[MAXN];
int main()
{
scanf("%d", &n);
for(int i = 0; i < n; ++i)
scanf("%d", &a[i]);
bool flag = true;
int ans = 0, t = 0, i;
for(i = 0; i < n-1; ++i)
{
t = i;
if(a[i] > a[i+1]) break;
}
if(i != n-1)
{
for(int i = t+1; i < n; ++i)
{
ans++;
if(a[i] > a[(i+1)%n])
{
flag = false;
break;
}
}
}
if(flag)
printf("%d\n", ans);
else
printf("-1\n");
return 0;
}
C. Little Pony and Expected Maximum
Twilight Sparkle was playing Ludo with her friends Rainbow Dash, Apple Jack and Flutter Shy. But she kept losing. Having returned to the castle, Twilight Sparkle became interested in the dice that were used in the game.
The dice has m faces: the first face of the dice contains a dot, the second one contains two dots, and so on, the m-th
face contains mdots. Twilight Sparkle is sure that when the dice is tossed, each face appears with probability 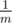 .
Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice n times.
.
Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice n times.
Output
Output a single real number corresponding to the expected maximum. The answer will be considered correct if its relative or absolute error doesn‘t exceed 10??-?4.
解题思路:
求数学期望,公式P = m - (1/m)^n - (2/m)^n - ... -((m-1)/m)^n
代码:
#include <cstdio>
#include <cstring>
#include <cmath>
int main()
{
int m, n;
scanf("%d%d", &m, &n);
double ans = m;
for(int i = 1; i < m; ++i)
ans -= pow(i*1.0/m, n);
printf("%.12f\n", ans);
return 0;
}
Codeforces Round #259 (Div. 2) 题解,布布扣,bubuko.com
Codeforces Round #259 (Div. 2) 题解
标签:codeforces round #25
原文地址:http://blog.csdn.net/u010084308/article/details/38346831

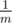 .
Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice
.
Also she knows that each toss is independent from others. Help her to calculate the expected maximum number of dots she could get after tossing the dice