标签:
题意。。看了很久。
其实就是用一个点n来连接其他联通分量,使得标号0~n-1这些点再一个联通分量中。
为了简化题目,假设原图中联通分量>=2,我们可以先找出原图中的环,因为按照题目规则,只有两个环分别拓展出一条边连接点n,使得所有联通分量和为1个联通分量。
下面解释一下样例3.
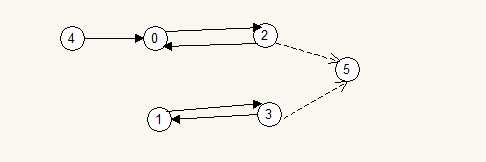
如图0,2是一个环 1,3是一个环。现在借助5把{4,0,2}和{1,3}这两个联通分量连接起来。先不考虑点4.那么{0,2}中有3种方案可以选择,{1,3}中有3中方案可以选则所以一共有9中方案。接下来考虑点4,那么挂上点4后,答案也是9. 所以种答案是18.
如果0~n-1这些点原来在一个联通分量中。那么 我们还要加上空集这种情况。
代码:
#include <cstdio> #include <cmath> #include <cstring> #include <ctime> #include <iostream> #include <algorithm> #include <set> #include <vector> #include <sstream> #include <typeinfo> #include <fstream> #define ll long long using namespace std; class Sunnygraphs2 { public: int vis[60]={0}; int used[60]={0}; vector<int>edge[60]; int num=0; void dfs(int u){ num++;used[u]=1; for(int i:edge[u])if(!used[i])dfs(i); } long long count(vector<int> a) { int n=a.size(); int m=n; for(int i=0;i<n;i++){ edge[i].push_back(a[i]); edge[a[i]].push_back(i); } dfs(0); ll ans=1; int cnt=0,mark=0,cur; for(int i=0;i<n;i++){//找环 if(!vis[i]){ cur=i;cnt=mark=0; for(int j=1;j<=50;j++){ cur=a[cur];cnt++;//记录环中节点数 if(cur==i){ mark=1;break; } } if(mark){ cur=i; for(int j=1;j<=50;j++){ vis[cur]=1; cur=a[cur]; } ans*=(ll)pow(2ll,cnt)-1; m-=cnt; } } } ans*=(ll)pow(2ll,m); if(num==n)ans++;//包含空集 return ans; } };
标签:
原文地址:http://www.cnblogs.com/pk28/p/5551100.html
- If he chose M = {}, the resulting graph contained the edges 0-1 and 0-1. The vertices 0 and 1 were in the same component.
- If he chose M = {0}, the resulting graph contained the edges 0-1 and 0-2. The vertices 0 and 1 were in the same component.
- If he chose M = {1}, the resulting graph contained the edges 0-1 and 1-2. The vertices 0 and 1 were in the same component.
- Finally, if he chose M = {0, 1}, the resulting graph contained the edges 0-2 and 1-2. And again, the vertices 0 and 1 were in the same component. (In the resulting graph we can still go from vertex 0 to vertex 1, even though we have to go via vertex 2.)
As all four choices of M are good, the correct answer is 4.